Принцып Дерехлея Даны две окружности, длина каждой из которых равна 100 см. На одной из них отмечено 100
точек, а на другой — несколько дуг, сумма длин которых меньше 1 см. Докажите, что эти
окружности можно совместить так, чтобы ни одна отмеченная точка не попала на отмеченную
дугу.
Другие вопросы по теме Математика
Популярные вопросы
- Прочитайте приведённый ниже текст, в котором пропущен ряд слов...
1 - Найди значение выражения 41x−20x+18x−26при x = 5....
2 - Кратвое содержание ключевые моменты Недоросль фонвизин...
3 - X+3/(x-2)(x+3) (x-3)(x-2)/x-2 (x^2+3x)/(x^2-9) (x^2-5x+6)/(x^2-4x+3)...
3 - Задача 7 остальные не нужны. Алгебра 7кл...
2 - Знайдіть координати вектора AB , якщо А(-3;2;-1), В(2;-5;3)....
2 - Всем привет вас мне это Всем привет вас мне это...
2 - Знайти область визначення функції f(x)=√x-5...
3 - За перше півріччя Оля і Дмитре отримали із оцінок 12. Оля отримала...
1 - Найди НОД(12;18). ответ: НОД...
1
Предположим обратное, то есть то, что невозможно окружности совместить так, чтобы ни одна отмеченная точка не попала на отмеченную дугу.
Совместим окружности. Назовем -тую точку
-тую точку  . Будем действовать следующим образом: в начальный момент хотя бы одна точка находится на дуге (пусть это точка
. Будем действовать следующим образом: в начальный момент хотя бы одна точка находится на дуге (пусть это точка  ). Начнем движение одной окружности относительно другой. Как только точка
). Начнем движение одной окружности относительно другой. Как только точка  сойдет с дуги, переключим внимание на другую точку
сойдет с дуги, переключим внимание на другую точку  , которая в этот момент находится на дуге. В каждый момент считаем прибором расстояние, которое проходит точка, за которой мы наблюдаем. Поэтому мы посчитаем расстояние
, которая в этот момент находится на дуге. В каждый момент считаем прибором расстояние, которое проходит точка, за которой мы наблюдаем. Поэтому мы посчитаем расстояние  , не превосходящее
, не превосходящее 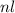 , где
, где 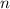 — количество точек,
— количество точек,  — суммарная длина дуг. С другой стороны, в любой момент прибор включен и считает расстояние. Поэтому
— суммарная длина дуг. С другой стороны, в любой момент прибор включен и считает расстояние. Поэтому  не меньше
не меньше  — длины окружности. Имеем:
— длины окружности. Имеем:  , однако
, однако  . Противоречие.
. Противоречие.