Пример по математике с тригонометрией
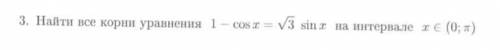
Другие вопросы по теме Математика
Популярные вопросы
- Напишите детскую сказку или рассказ о редком животном казахстана. соблюдайте...
1 - Напишите собственную смешную или анекдот.объём 6-8 предложений....
3 - Из предложений выписать словосочетания c вопросами(ручей укрылся толстым...
3 - Дуже терміново твір на одну з цих тем - своє рідне- своєрідне -чи можуть...
1 - Реферат на тему: растения красной книги луганщины...
2 - Примочите решить по действиям...
1 - Найдите массовую долю углерода в молекулах: а)пропана б) пропилена...
2 - Ag+hcl= mn+h3po4= решите по порядку.. это овр...
1 - Впоход собрались идти 48 мальчиков и 26 девочек. вожатый построил их...
1 - Знайдіть координати кінця напрямленого відрізка cd, який відповідає...
2
Пошаговое объяснение:
1-cosx=(√3)sinx
возведем в квадрат
(1-cosx)²=((√3)sinx)²
1-2cosx+cos²x=3sin²x
sin²x=1-cos²x
1-2cosx+cos²x=3(1-cos²x)
1-2cosx+cos²x=3-3cos²x
3cos²x-3+1-2cosx+cos²x=0
4cos²x-2cosx-2=0
разделим на 2
2cos²x-cosx-1=0
обозначим cosx=y
2y²-y-1=0
y₁₋₂=(1±√(1+8))/4=(1±√9)/4=(1±3)/4={-1/2;1}
1) y=-1/2
cosx=-1/2
x=±arccos(-1/2)+2kп=±(2п/3)+2kп, k∈Z
выберем корни на интервале (0;п)
при k=0
x=2п/3
2) y=1
cosx=1
x=2пm, m∈Z
на интервале (0;п) корней нет
ответ х=2п/3