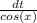Применяя указанные подстановки, найти следующие интегралы: 1) ∫x(5x^2-3)^7dx, 5x^2-3=t
2) ∫xdx/(sqrt(x+1)), (sqrt(x+1))=t
3) cos xdx /(1+sin^(2)x), sin x = t
Другие вопросы по теме Математика
Популярные вопросы
- Изучите новые слова. Прочитайте и переведите предложения с новой лексикой....
1 - решить мне эту контрольную!...
1 - Поставьте деепричастный оборот в нужное место в предложении, расставьте...
3 - Назвіть країни Америки у яких велику роль в енергетиці відіграють гідроресурси...
3 - Природная особенность дальнего востока : 1) Временные ресурсы 2)биологические...
1 - Равновесная цена устанавливается на рынке только в кратко периоде?...
3 - Ребята, посоветуйте порн@ фильмы, и напишите что будет если др@чить ?...
3 - Запишіть події з твору Усмішка Фантастичні - Реальні -...
3 - Задание: От существительных образуйте форму именительного падежа множественного...
3 - Білий кінь збунтувався тому що...
2
Пошаговое объяснение:
1)
t=5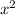 -3
-3
dt=5x*dx
dx=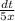
2)
t=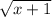
dt=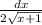
dx=2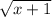 dt
dt
3)
t = sin x
dt = cos(x)dx
dx=