Прикаких натуральных n число 8n+3 делится на 13
Другие вопросы по теме Математика
Популярные вопросы
- Вычислите объема водорода (н.у), который выделяется при взаимодействии...
3 - Решите уравнение х^2-10х+21=0 если уравнение имеет более одного...
3 - Сообщение на тему группа лишайники по биологии...
3 - Составе рассказ от имени финикийца о морском путешествии...
2 - Асан қайғы туралы кластер керек еді....
2 - Вкаком субъекте находится сургутская грэс...
2 - Составить предложения, используя past progressive: 1. a man/to...
2 - Один з металів відкритих у 19 столітті назвали індієм .чому?...
1 - Составте цепь питания в зоне пустыне...
3 - Уосы обыкновенной ротовой аппарат грызущий или лижущий?...
3
8n+3=13k k-натуральное
8n=13k-3
8n=16k-3k-3
8n=16k-3(k+1)
(k+1) должно делиться на 8
k+1=8m m-натуральное
k=8m-1
8n+3=13(8m-1)
8n+3=104m-13
8n=104m-16
n=13m-2 m-натуральное
данная задача равносильно нахождению натуральных решений диофантового уравнения
частное решение 13*(-1)-8*(-2)=3;k=-1; n=-2
общее решение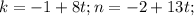 t є Z
t є Z
отсюда видно, что при n=-2+13t, t є N число 8n+3 делится на 13.