При каком значении параметра t система линейных уравнений совместна? Очень круто бы было видеть решение
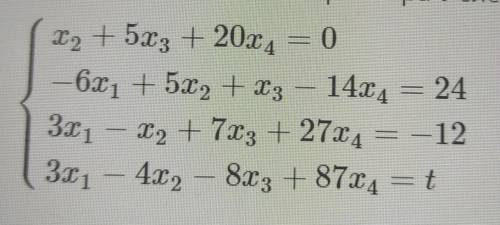
Другие вопросы по теме Математика
Популярные вопросы
- Какой экологический фактор ограничивает распространение растений на большую...
1 - Как получить стирол из неорганических веществ...
1 - 1) на каком из теплопередачи основано нагревание твердых тел? а. теплопроводность...
3 - Укажите промежуток которому принадлежит корень уравнения sqrt(4-3x)=5...
1 - Виконайте по діям (1 ціла одна третя + 0.5) помножити на сім восьмих...
2 - Теплоемкость идеального газа одноатомного газа при постоянном давлении...
3 - Два одинаковых теплоизолированных сосуда соединены трубкой с закрытым...
1 - Какие организмы относятся к царству дробянки?...
2 - Найдите радиус окружности,если она проходит через точку (-2; 1) и ее...
1 - Найдите площадь прямоугольника, если одна из его сторон равна 5 см, а...
2
2x + y = 4 - уравнение (1)
3x - 2y = -t - уравнение (2)
Наша задача - определить значение параметра t, для которого данная система уравнений будет иметь решение, то есть будет совместной.
Для начала рассмотрим метод решения данной системы уравнений - метод Крамера. Он позволяет вычислить значения искомых переменных (x и y) через определители.
1. Найдем определитель главной матрицы системы.
Главная матрица - это матрица, состоящая из коэффициентов при переменных.
Для данной системы уравнений главная матрица будет выглядеть так:
| 2 1 |
| 3 -2 |
Определитель главной матрицы (D) можно вычислить по формуле:
D = (2 * -2) - (1 * 3)
D = -4 - 3
D = -7
2. Теперь найдем определитель матрицы, в которой заменили первый столбец главной матрицы столбцом свободных членов (4 и -t).
Такая матрица будет выглядеть так:
| 4 1 |
| -t -2 |
Определитель этой матрицы (Dx) можно вычислить аналогичным образом:
Dx = (4 * -2) - (1 * (-t))
Dx = -8 + t
Dx = t - 8
3. Теперь найдем определитель матрицы, в которой заменили второй столбец главной матрицы столбцом свободных членов.
Такая матрица будет выглядеть так:
| 2 4 |
| 3 -t |
Определитель этой матрицы (Dy) можно также вычислить по формуле:
Dy = (2 * (-t)) - (4 * 3)
Dy = -2t - 12
4. Последний шаг - вычисляем значения искомых переменных x и y.
x = Dx / D
x = (t - 8) / (-7)
y = Dy / D
y = (-2t - 12) / (-7)
Теперь, чтобы система уравнений была совместной, необходимо, чтобы определитель главной матрицы (D) был неравен нулю.
D ≠ 0
-7 ≠ 0
Определитель главной матрицы не равен нулю для всех значений параметра t. Поэтому данная система уравнений совместна для любого значения параметра t.
Надеюсь, мое объяснение было понятным и подробным. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их!