При каком значении параметра a уравнение x^3 +3x^2 -9x -a=0 имеет два корня

-5, 27

Пошаговое объяснение:

Рассмотрим функцию . Её производная равна 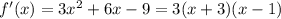. Производная равна нулю в точках x = -3, x = 1. При x ≤ -3 и x ≥ 1 производная неотрицательна, то есть функция возрастает, при -3 ≤ x ≤ 1 производная неположительна, то есть функция убывает. f(-3) = 27, f(1) = -5. Значит, функция имеет следующий вид (см. рис.)

Функция y = a — прямая, параллельная оси Ox. Как видно из графика, одно решение (пересечение) — при a < -5, a > 27; два решения — при a = -5, a = 27; три решения — при -5 < a < 27.