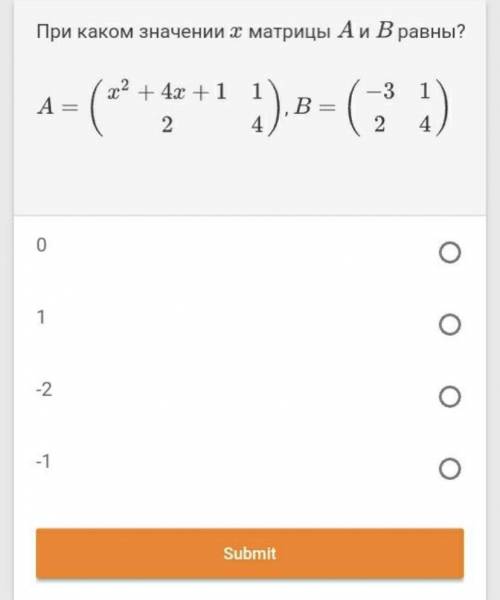
При каком значении х матрицы А и В будут равны
Другие вопросы по теме Математика
Популярные вопросы
- Напишите сочинение на тему посещение (какого нибудь места) не надо писать...
1 - Решить sinx=1/2 на отрезке от 0 до 2п...
2 - 2. ввести два числа. сравниваются два числа. то число, которое больше, если...
1 - Подскажите решения на птицеферме 17612 кур что в 28 раз больше чем уток а...
3 - Написать 10 предложений про свой любимый праздник, и как ты его празднуешь....
1 - Пусть α и β - углы треугольника. известно, что, 58° α 59°; 102°...
2 - Опишите правило работы с буфером обмена?...
1 - Решите по действиям (4,214: 0,14-5,436: 1,8)*0,1+1,6...
1 - Вычисли произведение, если один из множителей 803, и он на 83 меньше второго...
2 - Вчём сходство и отличие суходольных и пойменных лугов...
3
1. Сначала выполним умножение матрицы A на х:
A * х = |1 6 | * х = |1х 6х |
|3 x | |3х xх |
2. Теперь умножим матрицу В на х:
B * х = |2 4 | * х = |2х 4х |
|x -1 | |xх -х |
3. Затем приравняем полученные матрицы A * х и B * х и решим уравнение:
A * х = B * х
|1х 6х | = |2х 4х |
|3х xх | |xх -х |
Для этого вычтем из первой матрицы вторую матрицу:
|1х - 2х 6х - 4х | = |0 2х |
|3х - xх xх + х | |-x 2x |
Упростим полученную матрицу:
|- х 2х | = |0 2х |
|2х х | |-x 2x |
Теперь составим систему уравнений, приравняв каждый элемент матрицы:
-х = 0
2х = 2х
х = -x
х = 2x
Первое уравнение говорит о том, что -х должно равняться 0, значит х = 0.
Вторая и третья строки ставят равенство 2х с 2х и х с -х. Чтобы это выполнялось для любого значения х, необходимо чтобы x = 0.
Таким образом, матрицы A и B будут равны при значении х=0.