При каком значении b график функции y=bx2 проводит точку: можно решение?

Ответы

DanilPak2002 18.11.2020 07:34

Пошаговое объяснение:

Лемма Если график функции y=f(x) проходит через точку A(x_0;y_0) , то равенство y_0=f(x_0) верное

Доказательство напрямую следует из определения графика функции.

Графиком функции y=f(x) называют множество точек A(x_0;y_0) , координаты которых удовлетворяют уравнению y_0=f(x_0)

Пусть f(x)=bx^2 , где b - какая-то константа. Тогда:

1) Для точки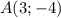 A(3;-4) по Лемме верно равенство -4=b*3^2 тогда $\displaystyle b=-\frac49$

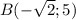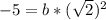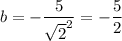
2) Для точки $B(-\sqrt2;5)$ по Лемме верно равенство $-5=b*(\sqrt2)^2$ тогда $\displaystyle b=-\frac5{\sqrt2^2}=-\frac52$

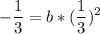3) Для точки $\displaystyle C(\frac13;-\frac13)$ по Лемме верно равенство $\displaystyle -\frac13=b*(\frac13)^2$ тогда $\displaystyle b=-\frac{\frac13}{\frac19}=-\frac93=-3$

4) Для точки D(10;20) по Лемме верно равенство 20=b*(10)^2 тогда $\displaystyle b = \frac{20}{100}=\frac2{10}=\frac15$

ПОКАЗАТЬ ОТВЕТЫ

eniyo2005 22.01.2024 16:02

Для того чтобы график функции y = bx^2 проходил через данную точку, необходимо чтобы координаты этой точки удовлетворяли уравнению функции.

Заданная точка имеет координаты (2, 0). Это означает, что x = 2 и y = 0.

Подставим эти значения в уравнение функции y = bx^2 и получим:

0 = b * 2^2

0 = 4b

Теперь решим полученное уравнение относительно b:

4b = 0

b = 0 / 4

b = 0

Таким образом, график функции y = bx^2 проходит через заданную точку, если b = 0.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика