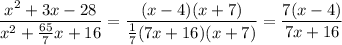При каком значении « а» можно сократить следующую дробь: числитель х в квадрате +3х-28. знаменатель: х в квадрате +ах+16. дробь нужно сократить. если значений « а» несколько - найти сумму. за .
Другие вопросы по теме Математика
Популярные вопросы
- Северная америка 1. каков общий характер поверхности? чем его можно...
1 - Богатство нашего региона.(по познанке)...
2 - Какие народы входят в состав рф? найдите информацию в интернете о...
1 - Уравнение реакции бутана и гексана....
3 - 1. как называется одна гласная которая тянется на несколько звуков?...
1 - Решить с объяснениями: -0,6+4; -0,4+1; -0,1+1; -0,7+1; -0,5-6,4; 3,8-10;...
2 - Розберіть за будовою і визначте б творення слова найстрашніша 20 ів)...
2 - Что такое крещение 4 класс окружающий мир...
3 - Словом аромат записано некоторое натуральное число. при этом разные...
1 - Определите время предложения.переделайте предложения из формы настоящего...
1
Разложим числитель
Значит, x = 4 и x = -7 - корни многочлена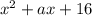 и при этом остаток от деления многочлена на двучлен равен нулю. Подставив x = 4 и x = -7, получим
и при этом остаток от деления многочлена на двучлен равен нулю. Подставив x = 4 и x = -7, получим
Сумма значений a: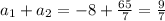
Для а = -8: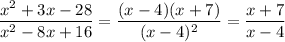
Для a = -65/7: