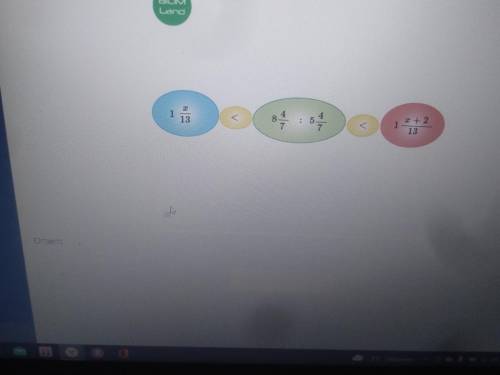
При каком наибольшем натуральном значении х будет верно неравенство
Другие вопросы по теме Математика
Популярные вопросы
- Коллаборационистер деген атау кімдерге берілді? Дам 20 б...
1 - Суммативная работа по всемирной истории для 4 четверти, 2 вариант 1 задание...
1 - 1. Прочитайте внимательно текст. В Солнечной системе, я знаю, есть восемь...
1 - 2 класс.литература стр69-72.прочитать составить план...
3 - 6.Укажите строку с глаголами 2 спряжения 2 лица: * 1)встреча...шь, мёрзн...шь2)тревож...те,...
2 - 46. «Ұлттың болашағы ана тілінде» деген тақырыпта сөйлеуге да- йындал....
2 - Для чего, по вашему мнению, автору понадоби1. Напишите продолжение данного...
1 - Решите неравенство (х-3)(х-2) 0...
2 - Карамен жазылған сөздерді я синонін тауып жаз Сонгы сөйлема сөйлем мүшесіне...
3 - Задание 1. Составьте правильно пищевую цепь из предложенных элементов:...
3
Мы имеем неравенство |2x - 5| < 7. Чтобы решить это неравенство, мы разобьем его на два случая:
1. Когда выражение 2x - 5 в модуле положительно: 2x - 5 > 0.
2. Когда выражение 2x - 5 в модуле отрицательно: -(2x - 5) > 0, что равносильно 2x - 5 < 0.
1. Для случая, когда 2x - 5 > 0, мы можем решить неравенство непосредственно:
2x - 5 < 7
2x < 12
x < 6.
2. Для случая, когда 2x - 5 < 0, мы решим неравенство, поменяв знак неравенства и перенеся -5 в другую сторону:
-(2x - 5) > 7
2x - 5 < -7
2x < -2
x < -1.
Таким образом, мы получили два множества решений неравенства:
- бесконечно много значений x меньше 6,
- бесконечно много значений x меньше -1.
Но нас интересует максимальное натуральное значение x. Натуральные числа - это положительные целые числа. Ответом на эту задачу будет наибольшее натуральное число, которое меньше 6 и меньше -1. Такого числа нет, потому что ни одно натуральное число не может быть одновременно меньше 6 и меньше -1.
Итак, отсутствует натуральное значение x, при котором неравенство |2x - 5| < 7 будет верным.