При каких значениях параметра a уравнение √(|x-2|) = √(a*x+1) имеет более одного решения? нужно подробное решение

Раз область значений функций левой и правой части уравнения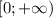 , то, приравняв левую и правую части уравнения к нулю, получим 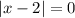и 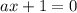 откуда  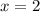и  - одно решение

Левая часть - под коренное выражение неотрицательно, т.е. уравнение будет зависеть только от правой части.

Возводим левую и правую части уравнения в квадрат

При условии, что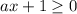 , возводим снова в квадрат обе части уравнения:

В левой части применим формулу разности квадратов:

Произведение равно нулю, если хотя бы один из множителей равен нулю.

откуда

откуда

Теперь исследуем на условии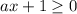 . Подставляем первый корень

Решением этого неравенства является промежуток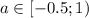

Подставим теперь второй корень.

решением этого неравенства является промежуток

Пересечение этих двух решений: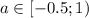 . Из выше сказанного при а = -0,5 уравнение имеет одно решение. Поэтому при данное уравнение имеет более одного решения.

ответ: при a ∈ (-0.5;1).

Для разнообразия графический метод, потому что он для ленивых