При каких значениях параметра а уравнение имеет единственное решение? ( ответ отмечен, мне нужно решение)

При каких значениях параметра а уравнение имеет единственное решение? ( ответ отмечен, мне нужно реш

Ответы

Димооон04 15.10.2020 16:08

-1

Пошаговое объяснение:

Заметим, что если x является решением уравнения, то и -x также является решением уравнения (действительно, возведение в квадрат, в четвёртую степень и взятие косинуса "убивает" минус). Значит, необходимое условие единственности решения: x = -x ⇒ x = 0 (условие не достаточное, так как помимо 0 могут быть и другие решения, поэтому каждое значение параметра необходимо будет проверить).

Подставим x = 0 в уравнение:

$0^4-2\cdot 0^2+a(7\cos{0}-2\cdot 0^2)+7a^2=0\\7a+7a^2=0\\7a(a+1)=0\\a=-1;0$

Если a = 0, то уравнение имеет вид:

$x^4-2x^2+0\cdot (7\cos{x}-2x^2)+7\cdot 0^2=0\\x^4-2x^2=0\\x^2(x^2-2)=0\\x=0;\pm\sqrt{2}$

Три решения, a = 0 не подходит.

Если a = -1:

$x^4-2x^2-(7\cos{x}-2x^2)+7\cdot(-1)^2=0\\x^4-7\cos{x}+7=0\\x^4=7(\cos{x}-1)$

Заметим, что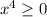 $x^4\geq 0$ , а $\cos{x}-1\leq 0$ , то есть левая часть не меньше нуля, а правая — не больше нуля. Равенство достигается, когда обе части равны нулю:

$\displaystyle\left \{ {{x^4=0,} \atop {7(\cos{x}-1)=0}} \right. \left \{ {{x=0,} \atop {7(\cos{0}-1)=0}} \right. \Rightarrow x=0$ — единственное решение. a = -1 подходит.