При каких значениях параметра а уравнение a*3^(2x+1)-(6a-4)*3^x+3(a-1)=0 имеет единственный корень?

Рассмотрим два случая

1) Если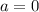 , то откуда .

2) Если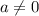 , то данное уравнение равносильно следующему уравнению , где 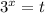, причём

при откуда 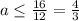квадратное уравнение имеет корни.

Чтобы данное уравнение имело единственный корень, нужно чтобы корни квадратного уравнения относительно были разных знаков. По теореме Виета:

⇒   откуда

С учётом того, что при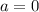 уравнение имеет единственный корень, то включая значение a = 0 в неравенстве 0 < a < 1, получаем 0 ≤ a < 1.

ответ: при a ∈ [0;1).