1. Математика
  2. При каких значениях b

При каких значениях b уравнения |x^2-5x+6|=b имеет ровно 3 решения

danasveshnikova danasveshnikova    2   27.09.2019 01:50    0

Ответы
мак122 мак122  11.08.2020 07:51

При условии,что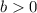 b0 возведем в квадрат обе части уравнения, имеем:

(x^2-5x+6)^2=b^2\\ (x^2-5x+6)^2-b^2=0\\ (x^2-5x+6+b)(x^2-5x+6-b)=0

Произведение равно нулю, если хотя бы один из множителей равен нулю.

x^2-5x+6+b=0~~~\big(\star\big)\\ x^2-5x+6-b=0\big(\star \star\big)

Это уравнение будет иметь три решения, если один из этих уравнений D>0 и D=0


Найдем дискриминант квадратного уравнения \big(\star\big)

D=25-4(6+b)=25-24-4b=1-4b

и уравнения \big(\star \star\big)

D=25-4(6-b)=25-24+4b=1+4b



\displaystyle \left \{ {{1-4b0} \atop {1+4b=0}} \right. ~~~\Rightarrow~~~\left \{ {{b


или


\displaystyle \left \{ {{1-4b=0} \atop {1+4b0}} \right. ~~~\Rightarrow~~~ \left \{ {{b=0.25} \atop {b-0.25}} \right. ~~~\Rightarrow~~~ b=0.25


Значение b = -0.25 не удовлетворяет условию, ведь b > 0.

ответ: b =  0,25.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Laura11111111111 Laura11111111111  27.06.2019 13:00
Мороженое содержит 60 % воды, 19 % молочного жира, остальное - сахар. сколько граммов сахара потребуется для приготовления 2,5 кг мороженого...
ruks777 ruks777  27.06.2019 13:00
Вчетырёх ящиках 86 кг яблок : в первом ящике и во втором поровну, в третьем ящике 20 кг, а в четвёртом 18 кг.узнай, сколько кг яблок в первом ящике. объясните, что...
Bayana000 Bayana000  27.06.2019 13:00
Где лучше всего строить обсерваторию для оптического наблюдения за ? на берегу моряв крупном городев горахна равнине...
vlmx2freddy vlmx2freddy  27.06.2019 13:10
Найдите моду ряда чисел : 1 6 23 25 38 45 76 78 5 25 12 44 25...
dias2050 dias2050  27.06.2019 13:10
2во 2 степени умножить на 4 в 8 степени/ на 16 в 5 степени умножить на 5 во 2...
vadim1154 vadim1154  27.06.2019 13:10
1612.выполните действия: а)(3,8*1,75: 0,95-1,02): 2,3+0,4=? б)(11,28+3,4: 0,85*1,55): 4,6-0,8=? зарание...
mistrgeniy mistrgeniy  27.06.2019 13:10
Общая масса трех кусков гранита 156 кг кусок серого гранита тяжелее куска красного гранита на 18 килограмм ,а кусок красного гранита легче куска белого на 15 кг найди...
fgggg2qq fgggg2qq  27.06.2019 13:10
Очeнь ! раскройте скобки и подобные слагаемые: а)0,2(6х-5)-4(0,2х-2); б) 0,4(1,5y+3)-2,5(3-0,6y); в) 2/9(1,8m-5,4)-3/7(2,1m-4,2); с полным ! приличные только !...
avernius avernius  27.06.2019 13:10
Купили гусей.два из них имеют массу по 4 кг, три по 3,5 кг и один 3,1 кг. найдите среднюю массу купленных гусей...
Alinysikmania1234567 Alinysikmania1234567  27.06.2019 13:10
«школі подарували 56 матчів .1/4 всіх мячів використовують на своїх уроках учні початкових класів.скільки мячів використовують учні середніх і старших класі...

Популярные вопросы