При каких значениях b, уравнение 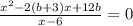не имеет решений​

ответ в приложении.

Пошаговое объяснение:

1) Рассмотрим случай, когда у уравнения будет один корень. В этом случае b=3, подставляем в исходное уравнение, получаем, что корнем является 6, но это посторонний корень, значит, корней нет.

2) Рассмотрим случай, когда у уравнения нет корней, то есть дискриминант меньше нуля. Таких значений нет.

3) Рассматривать случай, когда дискриминант больше 0 не имеет смысла, потому что у нас всегда будет два или один (в том случае, когда один из корней посторонний) корней.