Преобразовать в произведение следующие выражения: 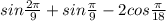
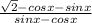
3-4cos4x+cos8x-8cos^4*2x
ответы:
1.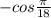
2.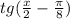
3.-8cos4x
Другие вопросы по теме Математика
Популярные вопросы
- Почему при работе с информацией необходимо соблюдать этические нормы?...
1 - Найдите молекулярную формулу соединения состав кторого следующий: углерода...
3 - Из каких двух слагаемых должна состоять сумма чтобы её значение равнялось...
1 - Чему равно расстояние от северного полюса до южного по поверхности земли...
3 - 4. замените словосочетание «ремесло сапожника«, построенное на основе , синонимичным...
2 - Площадь равностороннего треугольника равна 25корень3. вычислите сторону треугольника...
1 - На формирование каких новых взглядов влиял галилео галилей...
3 - 2. укажите источники информации, которые, на ваш взгляд, наиболее распространены...
3 - Сложить 5 вопросительных и 5 повествовательных предложений в passive voice-...
2 - Какое нибудь растение и ее паспорт например 1.название- аллоя древовидная...
1
1.sin2π/9+sinπ/9-2cosπ/18=(sin2π/9+sinπ/9)-2cosπ/18=
2sinπ/6*cosπ/18-2cosπ/18=2*0.5cosπ/18-2cosπ/18=-cosπ/18
2. (√2-cosx-sinx)/(sinx-cosx)=(√2-(sinx+sin(π/2-x)))/(sinx-sin(π/2-x))=
(√2-2sinπ/4*cos((x-π/4)))/(2sin(x-π/4)*cosπ/4)=
√2(1-cos((x-π/4))/(√2*sin(x-π/4))=2sin²(x/2-π/8)/((2sin(x/2-π/8)*(cos(x/2-π/8))=
sin(x/2-π/8)/((cos(x/2-π/8))=tg(x/2-π/8)
3. 3-4cos4x+cos8x-8cos⁴2x= 3-4cos4x+cos²4x-sin²4x-2*(1+cos4x)²=
3-4cos4x+cos²4x-sin²4x-2-4cos4x-cos²4x=3-4cos4x+2cos²4x-1-2-4cos4x
-2cos²4x=-8cos4x