Преобразовать формулу так, чтобы она содержала только булевы операции, упростить
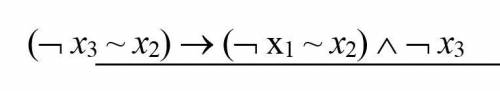
Другие вопросы по теме Математика
Популярные вопросы
- напишите диаграмму искусства рококо...
2 - Решить выберите правильный вариант ответа 1 my friend never listens to...
1 - Это надо составить план по главе маман из повести толстого...
3 - Для чего нужно заниматься самообразованием?...
3 - При каких температурах снег лежит на горах?...
3 - По реостату подключенному к источнику тока с напряжением u=36в проходит...
2 - Раскройте смысл высказывания учёного-. могли бы вы обосновать его справедливость...
3 - Абсолютное большинство хорошо подготовлены подготовлено к сдаче эказмена...
1 - Что означает по what,s your favourite animai&...
1 - Напишите 3 вопроса к произведению с.есенина ,,собаке качалова...
3
1. Раскрытие скобок:
(¬P ∨ Q) ∨ (¬P ∨ ¬Q)
2. Применение закона двойного отрицания (Double Negation Law):
(¬P ∨ Q) ∨ ¬(P ∧ Q)
3. Применение закона дистрибутивности (Distributive Law):
(¬P ∨ Q) ∨ (¬P ∨ ¬Q) ≡ (¬P ∨ ¬P) ∨ (¬P ∨ Q) ∨ (¬Q ∨ ¬P) ∨ (¬Q ∨ ¬Q)
4. Упрощение дублированных переменных:
(¬P ∨ ¬P) ∨ (¬P ∨ Q) ∨ (¬Q ∨ ¬P) ∨ (¬Q ∨ ¬Q) ≡ ¬P ∨ (¬P ∨ Q) ∨ (¬Q ∨ ¬P)
5. Применение закона идемпотентности (Idempotent Law):
¬P ∨ (¬P ∨ Q) ∨ (¬Q ∨ ¬P) ≡ ¬P ∨ Q ∨ (¬Q ∨ ¬P)
6. Применение закона коммутативности (Commutative Law):
¬P ∨ Q ∨ (¬Q ∨ ¬P) ≡ ¬P ∨ (¬Q ∨ Q) ∨ ¬P
7. Применение закона идемпотентности (Idempotent Law):
¬P ∨ (¬Q ∨ Q) ∨ ¬P ≡ ¬P ∨ ¬P ∨ Q
8. Применение закона коммутативности (Commutative Law):
¬P ∨ ¬P ∨ Q ≡ ¬P ∨ Q
Таким образом, упрощенная формула будет выглядеть как ¬P ∨ Q. Эта формула содержит только булевы операции и является упрощенной версией исходной формулы.