Представить в тригонометрической форме комплексное число 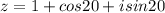
Син и Кос 20-градусов.
Другие вопросы по теме Математика
Популярные вопросы
- Сколько воздуха (в литрах) использует для дыхания 28 учеников...
1 - Що позначено біля верхньої рамок карти годинних поясів...
3 - Найти предел, используя эквивалентные бесконечно малые функции...
1 - Написать сочиненте про жизнь оастений летом из 5 !...
2 - Решите примеры с об яснением: 9+7,7+9,8+3,3+8,9+8,8+9....
2 - Чему равен угол,если вертикальный с ним угол равен 34°...
1 - Напишите небольшое сочинение на тему лес поздней осенью . нужно...
1 - Запишите определение послания в стихотворении к чаадаеву...
1 - Передвижение по краю проезжей части разрешено для и при...
2 - Осуществите цепочку превращений: so2← h2s ← s...
3
Пошаговое объяснение:
_________________________
Использованы формулы половинного аргумента