Правильные многоугольники 1.Сторона правильного вписанного многоугольника из центра окружности видна под углом 10°.
Сколько сторон у многоугольника?
Количество сторон:
2.В окружность вписан правильный треугольник ABC
Вычисли градусную меру дуги BA=
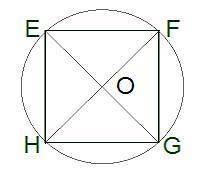
3.Вычисли неизвестные величины, если EFGH — квадрат со стороной 12 см.
R=
12
6√3
12√2
12√3
6
6√2
S(EFGH)= см^2

Добрый день! Рад принять роль школьного учителя и помочь вам разобраться с вопросами о правильных многоугольниках.

1. Сторона правильного вписанного многоугольника из центра окружности видна под углом 10°. Нам нужно найти количество сторон этого многоугольника.
Правильный многоугольник состоит из равных сторон и равных углов. Когда мы соединяем центр окружности с вершинами многоугольника, мы получаем радиус, который является подвижной линией и образует угол с каждой из сторон многоугольника.
Зная, что один из этих углов равен 10°, мы можем найти количество сторон многоугольника, используя следующую формулу:
Количество сторон = 360° / мере одного угла

Таким образом, количество сторон = 360° / 10° = 36 сторон.

Ответ: Многоугольник имеет 36 сторон.

2. В окружность вписан правильный треугольник ABC. Задача состоит в вычислении градусной меры дуги BA.
В правильном треугольнике каждый угол равен 60°. Дуга BA является частью окружности, и ее градусная мера будет равна градусной мере соответствующего центрального угла.
Таким образом, градусная мера дуги BA = 60°.

Ответ: Градусная мера дуги BA равна 60°.

3. Рассмотрим квадрат EFGH со стороной 12 см и вычислим неизвестные величины.
R - радиус описанной окружности вокруг квадрата. Радиус описанной окружности вокруг квадрата равен половине диагонали квадрата.
Длина диагонали квадрата можно найти по теореме Пифагора: д^2 = a^2 + a^2, где a - сторона квадрата.
В данном случае a = 12 см. Подставляем значения и находим длину диагонали:
д^2 = 12^2 + 12^2 = 144 + 144 = 288
д = √288 = 12√2 см

Таким образом, радиус описанной окружности равен половине диагонали:
R = 12√2 / 2 = 6√2 см.

S(EFGH) - площадь квадрата EFGH. Площадь квадрата можно найти как сторона, возведенная в квадрат.
S(EFGH) = 12^2 = 144 см^2.

Ответ:
R = 6√2 см
S(EFGH) = 144 см^2.

Я надеюсь, что мои объяснения были понятны и полезны. Если у вас есть еще вопросы, буду рад помочь!