1. Математика
  2. Построить схематический чертеж

Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:

2222381 2222381    3   28.02.2019 10:50    1

Ответы
elizapanfilova1 elizapanfilova1  23.05.2020 16:54

Как я понял условие, необходимо найти площадь фигуры ограниченной линиями: параболой у = x^2 + 4x - 4 и прямой: 12х-6у+24=0, или у = 2х+4.

Найдем абсциссы точек пересечения:

x^2+4x-4 = 2x+4

x^2+2x-8 = 0   По теореме Виета корни: -4  и  2.

Тогда исходя из рисунка:

S=|\int\limits^2_{-4} {(x^2+4x-4)} \, dx| \ \ +\ \ \int\limits^2_{-4} {(2x+4)} \, dx\ \ =

=\ |((x^3/3)\ +2x^2-4x)\ |_{-4}^2\ \ |\ \ +\ \ (x^2+4x)\ |_{-4}^2\ \ =\ \

=\ \ |((8/3)+8-8)-((-64/3)+32+16)|\ +\ (4+8)\ -\ (16-16)=

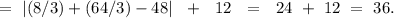
==\ |(8/3)+(64/3) - 48|\ \ +\ \ 12\ \ =\ \ 24\ +\ 12\ =\ 36.

ответ: 36.

Не идут вложения. Пришлите эл. адрес. Вышлю иллюстрацию туда.

ПОКАЗАТЬ ОТВЕТЫ
mrdaaly mrdaaly  23.05.2020 16:54

После упрощения первая линия задается формулой у=х²+4х-4, вторая - у=2х+4.

Площадь фигуры находим, используя интеграл.

Находим абсциссы пересечения графиков.

х²+4х-4=2х+4

х²+2х-8=0

х₁=-4, х₂=2

\int\limits^2_{-4} {(2x+4-x^2-4x+4)} \, dx = \int\limits^2_{-4} {(-x^2-2x+8)} \, dx =

(-\frac{x^3}{3}-x^2+8x) I^2_{-4} = 

= -\frac{8}{3}-4+16-(\frac{4^3}{3}-16-32)=12+48-24=36

К сожалению, файл с чертежом не прикрепляется.

ответ. 36

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
lolkek142 lolkek142  13.08.2019 03:00
Вставте одну цифру 2,3 или 4, чтобы числа 2_5 и 21 были взаимно простыми...
natalia1676 natalia1676  13.08.2019 03:00
при каких значениях а система уравнений имеет одно решение...
Дашенька66778 Дашенька66778  13.08.2019 03:00
Митя ,коля и дима писали сочинение. митя написал его за 3660 с,коля -за 65 мин, а дима - за 1 ч. кто быстрее всех написал сочинение?...
Айымгул1 Айымгул1  13.08.2019 02:50
Как и почему расизм менялся со временем ,...
ruan ruan  13.08.2019 02:50
Як медоносні бжоли готуються до зими ?...
zatzepinanatas zatzepinanatas  13.08.2019 02:50
1.простейшие обусловлены влиянием на кожу a) эфирного масла b) кислорода c) температурного фактора d) вакуумного воздействия 2.механизм действия процедур a) болеутоляющий b) антиаллергический...
аааликкк аааликкк  13.08.2019 02:50
Вкафе - 2 зала вместимостью 25 человек и 34 человека. какой будет минимальный доход кафе за один день, если оба зала будут максимально заполнены, а сумма минимального чека с человека...
adinakuba adinakuba  13.08.2019 02:50
Как решить пример в столбик 123×456...
vqhboqvqw vqhboqvqw  13.08.2019 02:50
Исследуйте свой дом (квартиру) и запишите всё, что, на ваш взгляд, изготовлено из минералов. подсказка: у вас на кухне есть соль? из чего сделаны оконные стёкла? что находится в карандаше?...
Snyezha Snyezha  13.08.2019 02:50
Скажите, у госпожи удача имеются ли сестры (сестра) ? назовите такую сестру ?...

Популярные вопросы