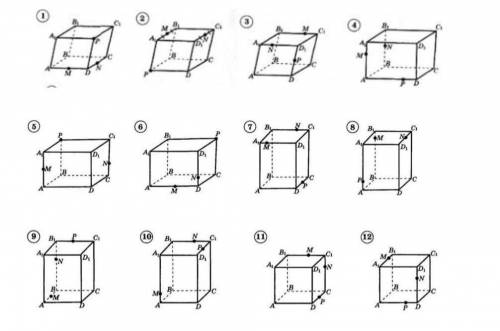
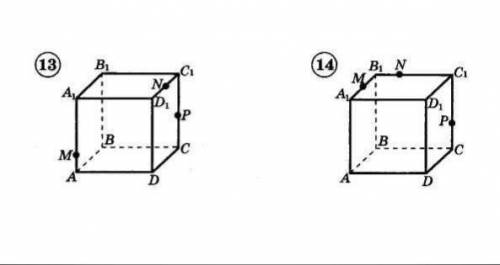
Построить сечения параллелепипеда по трем заданным точкам

Для построения сечений параллелепипеда по заданным точкам, мы должны использовать информацию о положении этих точек относительно параллелепипеда.

1. Вначале, давайте разберемся, что такое сечение параллелепипеда. Сечение параллелепипеда - это плоская фигура, полученная пересечением параллелепипеда с плоскостью.

2. У нас есть три заданные точки, обозначенные как A, B и C на рисунке. Для построения сечений, нам потребуется выбрать плоскость, такую что все эти точки будут лежать на ней.

3. Процедура построения сечений:

a) Найдите третью точку, образующую диагональ с уже заданными точками. Например, третья точка для A и B будет обозначаться как D, для A и C будет обозначаться как E, и для B и C будет обозначаться как F.

b) Найдите центр плоскости, проходящей через точки A, B и C. Для этого построим перпендикуляр от середины отрезка AC к прямой BF и найдем точку пересечения. Обозначим центр плоскости как O.

c) Найдите нормаль к плоскости, проходящей через точки A, B и C. Для этого можно построить векторы AB и AC, а затем найти их векторное произведение. Обозначим эту нормаль как n.

d) Построим нашу плоскость, используя точку O как точку на плоскости и вектор n как нормаль к плоскости. Тогда полученная плоскость будет пересекать параллелепипед в искомых сечениях.

4. Определение результата:

a) Первое сечение (A1B1C1). Для этого мы должны найти точки пересечения плоскости с ребрами параллелепипеда, проходящими через заданные точки A, B и C. Необходимо найти точки пересечения плоскости с отрезками AB, AC и BC, и соединить эти точки друг с другом. Полученная фигура и будет первым сечением.

b) Второе сечение (A2B2C2). Для этого мы должны найти точки пересечения плоскости с другими ребрами параллелепипеда, проходящими через заданные точки A, B и C. Необходимо найти точки пересечения плоскости с отрезками AD, AE и DF, и соединить эти точки друг с другом. Полученная фигура и будет вторым сечением.

c) Третье сечение (A3B3C3). Для этого мы должны найти точки пересечения плоскости с оставшимися ребрами параллелепипеда, проходящими через заданные точки A, B и C. Необходимо найти точки пересечения плоскости с отрезками BF, CF и CE, и соединить эти точки друг с другом. Полученная фигура и будет третьим сечением.

В итоге, мы получим три разных сечения параллелепипеда, образованные заданными точками A, B и C.

Надеюсь, это объяснение помогло вам разобраться в процессе построения сечений параллелепипеда. Если у вас остались вопросы, не стесняйтесь задавать.