Построить график функции и записать ее свойства:
y=3x^5-5x^3
Другие вопросы по теме Математика
Популярные вопросы
- Кукует кукушка и хрюкает хрюшка а значит, кого-то лягает лягушка....
1 - Схема поздравления дикой утки по кличке белое зеркальце...
3 - Примеры духовной личности (общество 6 класс) 10...
3 - Нужен доклад по кубановедению на тему влияние человека на природу...
3 - Найти координаты точек пересечения прямых с осями координат. 1.y=x+1...
3 - Fill in the gaps with: some ,any,much,many. are there on the table?...
3 - Как решить? (звёздочка это 0,25*7,2*40...
3 - Составьте текст используя слово-сочетания: необычайная тишина,...
3 - Выразите 40% в виде дроби а)2/5 б)4/5 в)5/4 г)гругой ответ...
2 - Мяч брошен с начальной скоростью 20м/с по углом 30 градусов горизонту....
3
Задана функция
1) Найдем область определения функции:
2) Исследуем функцию на четность:
Функция нечетная, непериодическая.
3) Найдем точки пересечения графика функции с осями координат:
Если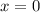 , то
, то  , значит
, значит 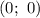 — точка пересечения с осью
— точка пересечения с осью 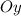 .
.
Если , то есть
, то есть 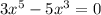 , то:
, то:
Значит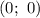 ,
, 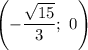 и
и 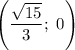 — точки пересечения с осью
— точки пересечения с осью 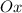 .
.
4) Асимптот данная функция не имеет, поскольку она непрерывная на всей области определения.
5) Найдем производную и критические (стационарные) точки функции:
Из уравнения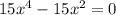 имеем критические точки:
имеем критические точки:
6) Найдем промежутки возрастания, убывания и экстремумы функции, заполнив таблицу (см. вложение).
7) Исследуем функцию на выпуклость и точки перегиба с второй производной:
Если на промежутке дифференцируемая функция
дифференцируемая функция 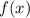 имеет положительную вторую производную, то есть
имеет положительную вторую производную, то есть 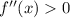 для всех
для всех 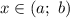 , то график этой функции на
, то график этой функции на  является выпуклым вниз; если на промежутке
является выпуклым вниз; если на промежутке  дифференцируемая функция
дифференцируемая функция 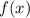 имеет отрицательную вторую производную, то есть
имеет отрицательную вторую производную, то есть 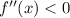 для всех
для всех 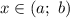 , то график этой функции на
, то график этой функции на  является выпуклым вверх.
является выпуклым вверх.
Решим уравнение: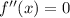
Имеем корни:
Систематизируем данные, полученные по второй производной, в таблице (см. вложение)
8) Изобразим график заданной функции (см. вложение).
9) Из графика можем найти область значений функции: