понять как расписывать (сокращать) факториалы и считать их?
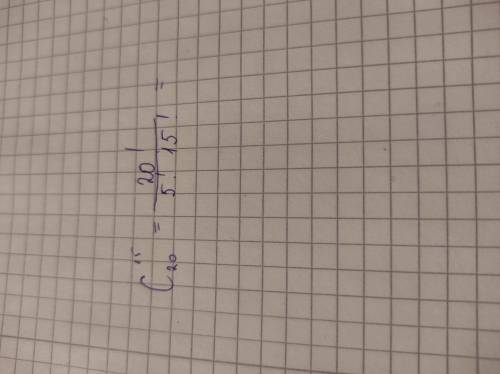
Другие вопросы по теме Математика
Популярные вопросы
- Как проспригать слово растаять в 1 спряжении...
1 - Втрапеции abcd ( ad паралельно bc ) известно , что ab = корень из...
2 - Оценка деятельности вещего олега современниками и...
1 - Когда состоялась первая кругосветная экспидиция?...
3 - Нужно написать краткое сочинение на 20 предложений по теме плюсы...
2 - При взаимодействии 0,662 литра алкена (н.у) с хлором образуется...
2 - Можно ли по внешниму виду растения определить состояниепроцесов...
3 - Придумать 6 предложений (2 бессоюзных,2 сложноподчинённых и 2 сложносочинённых)....
2 - Ширину прямоугольника увеличим на 25 процентов.на сколько процентов...
3 - Какие два города считались книжными центрами древней руси?...
2
n! = 1*2*3**(n - 1)*n
n! = (n-1)! * n = (n - 2)!*(n - 1)*n
20! / 5!*15! = 1*2*3*...*20 /(1*2*3*4*5 * 1*2*...*15) = 16*17*18*19*20 / 2*3*4*5 = 16*17*3*19 = 15504
20! это 1*2*3*4*5*6*7*8*9*10*11*12*13*14*15*16*17*18*19*20
5! это 1*2*3*4*5
15 по такому же принципу
и вот например как видишь в факториале 20 и 5 числа 1*2*3*4*5 одинковы, следовательно их можно сократить
когда распишешь факториал 15 там тоже будут повторяться числа с числами в 20!
и то, что останется не сокращённым нужно перемножить между собой
тут ответ будет 15504