Покозательные уравнения 1) 0,3^3x-2 =1. 2)6^3x * (1)/(6)=6*((1)/(6))^2x . 3) (5^x)-6*5^x +5=0
Другие вопросы по теме Математика
Популярные вопросы
- Что нельзя выпросить у скупердяя даже зимой?...
1 - Дано: угол aoe = 180°, aoc =142°, угол aob = bod, угол cod = doe. найти:...
1 - Деление каких клеток обеспечивает рост растения в толщину...
1 - Вода - основная среда для протекания реакций клетки. она - источник кислорода,...
2 - Какая связь в одинаковых простых веществах?...
1 - Портрет дмитрия донского 1-годы жизни (правления) 2-что сделал для государства...
3 - 1)как осуществить настройку браузера? 2)для чего нужна адресная строка в...
2 - Вчем состоит отличие растения от всех других живых существ...
2 - Надо найти экстремум методом множителей лагранжа. z = x×y² x² + 4×y² = 20...
1 - 2przyklady globalizacji no plaszczyznie ekonomicznej...
2
1)
(3/10)^3x=3
log₃ ((3/10)^3x)=log₃3
log₃ (3^3x)-log₃ (10^3x)=1
3x*1-3x*log₃ 10=1
3x(1-1/lg 3)=1
x=1/(3(1-1/lg 3))
2)
=
6^(3x-1)=1/6^(2x-1)
6^(3x-1+2x-1)=1
(5x-2)*log₆6=0
5x-2=0
x=2/5
3)
=
-5*5^x+5=0
-5*(5^x-1)=0
5^x=1
x*log₅5=0
x=0
1)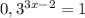
3x-2=0
3x=2
x=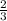
2)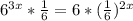
3x-1=1-2x
5x=2
x=0,4
3)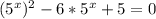
введем замену переменной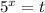
t²-6t+5=0
D=36-20=16
вернемся к замене переменной
1)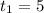
x=1
2)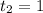
x=0