Показати, що вектори p, q, r утворюють базис тривимірного простору і знайти координати вектора x в цьому базисі
(13 Номер)

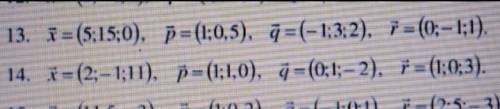
Показати, що вектори p, q, r утворюють базис тривимірного простору і знайти координати вектора x в ц

Ответы

123451175 25.04.2021 11:21

$\mathbf{\vec{x}(-5;2;2)}$

Пошаговое объяснение:

$\begin{vmatrix}1 &0 &5 \\ -1 & 3 & 2\\ 0 &-1 & 1\end{vmatrix}=3+5+2=10\neq 0$

Т.к. определитель не равен 0, то векторы составляют базис.

$\left\{\begin{matrix}x+5z=5\\-x+3y+2z=15\\ -y+z=0\\ \end{matrix}\right.\\$

y=z; из 3-го уравнения, подставим во 2-е

-х+3z+2z=15

-x+5z=15

сложим c 1-м

10z=20; z=2;

y=2;

x+10=5;x=-5

$\vec{x}(-5;2;2)$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

okm616 25.09.2021 01:18

21415тон = тон центнеров килограмм...

1FreeMad1 25.09.2021 01:18

Sashaooo 25.09.2021 01:20

Помине очень супер супер супер...

cat0708200416 25.09.2021 01:21

только решите всё и понятно....

sasha10072004 25.09.2021 01:30

Запишите ответ в НЕПРАВИЛЬНОЙ ДРОБИ...

BovolskajLesj 25.09.2021 01:34

нур92 25.09.2021 01:37

veraruu 25.09.2021 01:38

faceface96 01.02.2021 19:54

gggtair2004 01.02.2021 19:54

Показати, що вектори p, q, r утворюють базис тривимірного простору і знайти координати вектора x в цьому базисі(13 Номер)​