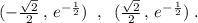Подробное решение найдите точки перегиба функции f(x) = 
Другие вопросы по теме Математика
Популярные вопросы
- Найдите площадь параллелограмма , стороны которого равны 10 см и 4см,...
3 - В первом задании нужно по частям речи (наречие, глагол)...
3 - С какой целью проводят кольцевание птиц?...
2 - При каких условиях стоит ухаживать за светлохвойными породами?...
3 - Решите графически уравнениеМного...
1 - с историей ! Только номер 4 и 5...
3 - Получению кислорода разложением перманганата калия соответствует уравнение...
1 - Приготовьте 80г 3% раствора KCl (калий хлор), решить как задачу...
2 - Что из перечисленного было характерно для экономического развития...
1 - , очень . Только без шуток, честно...
1
Точки перегиба: