1. Математика
  2. Под корнем х-1=х-3 решить

Под корнем х-1=х-3 решить уравнение !

bogdannazarenkomen bogdannazarenkomen    2   26.08.2019 04:00    1

Ответы
Аполлинарияполишка Аполлинарияполишка  09.09.2020 07:19

Решим с дискриминанта.

Выражение: D=b^2-4*a*c

Формулы корней: x_{1} =\frac{-b-\sqrt{D} }{2*a} \;\;\;\;\;\;\;x_{2} =\frac{-b+\sqrt{D} }{2*a}

Во 2 выражении используем формулу: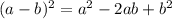 (a-b)^2=a^2-2ab+b^2

\sqrt{x-1}=x-3\\\\x-1=(x-3)^2\\\\x-1=x^2-6x+9\\\\x-1-x^2+6x-9=0\\\\7x-10-x^2=0\\\\-x^2+7x-10=0\\\\x^2-7x+10=0\;\;\;\;\;\boxed{a=1\;\;b=-7\;\;c=10}\\\\D=(-7)^2-4*1*10=49-40=9=3^2\\\\x_{1}= \frac{-(-7)-\sqrt{9}}{2*1} = \frac{7-3}{2}= \frac{4}{2} =2\\\\x_{2}= \frac{-(-7)+\sqrt{9}}{2*1} = \frac{7+3}{2}= \frac{10}{2}=5\\\\ODZ\\x=2\longrightarrow\sqrt{2-1}=2-3\longrightarrow 1=-1\longrightarrow x\neq 2\\x=5\longrightarrow \sqrt{5-1}=5-3\longrightarrow 2=2\longrightarrow x=5\\\\x \neq 2\;\;\;\;x=5\\\\x=5

ПОКАЗАТЬ ОТВЕТЫ
Аня3321 Аня3321  09.09.2020 07:19

{5}

Пошаговое объяснение:

\displaystyle \sqrt{x-1}=x-3

ОДЗ: x - 1 ≥ 0 ⇔ x ≥ 1.

Если x - 3 < 0 - нет решения. Пусть x - 3 ≥ 0, то есть x ≥ 3. Теперь можно возвести в квадрат:

\displaystyle \sqrt{x-1}=x-3 \Leftrightarrow (\sqrt{x-1})^{2}=(x-3)^{2} \Leftrightarrow x-1=x^{2}-6 \cdot x +9 \Leftrightarrow \\\\\Leftrightarrow x^{2}-7 \cdot x +10=0

D=(-7)²-4·1·10=49-40=9=3²

x₁=(7-3)/2= 4/2 = 2 < 3 - не подходит,

x₂=(7+3)/2= 10/2 = 5 > 3 - подходит.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
iadsodasdfs iadsodasdfs  30.06.2019 23:00
Решите уравнение. 3х+1 под корнем + х+3 под корнем= 18-2х под корнем...
sasharaiskaja sasharaiskaja  30.06.2019 23:00
Не могу вспомнить как найти корень уравнения. вот пример: -2+5х=10х+4...
encl3 encl3  30.06.2019 23:00
1. первичная реальность в неклассической философии представлена как … 1) духовная культура 2) жизнь человека 3) материальная культура 4) общественное производство 5) разум...
nastea030 nastea030  30.06.2019 23:00
4. учение о сверхчеловеке разрабатывал … 1) ницше 2) фихте 3) шеллинг 4) шопенгауэр...
ivasil2012 ivasil2012  30.06.2019 23:00
Решить уравнение 1) 2*/4-х/=9 2) -2целых1/5+х=-5целых1/2...
SillyLittleFool SillyLittleFool  30.06.2019 23:00
Теория вероятности 1) бросаются 2 игральные кости. какова вероятность того, что сумма очков, выпавших на этих костях,окажется равной 5 ? 2) в лотерее из 30 билетов 5 выигрышных. какова...
yurka1973 yurka1973  30.06.2019 23:00
Два ребра треугольного параллепипеда выходящие из одной вершины равны 2 и 6 . объём 48 . найдите третье ребро ? решение напишите , с формулами если можно...
fatowka84 fatowka84  30.06.2019 23:00
Вобменном пункте можно совершить одну из двух операций: 1) за две золотых монеты получить три серебрянные и одну деревянную; 2) за пять серебрянных монет получить три золотых и одну...
lizabolovinceva lizabolovinceva  30.06.2019 23:00
Цена товара повысилась на 25%. на сколько процентов необходимо снизить новую цену чтобы она сравнялась с первоначальной. полный ответ!...
Игорь5002 Игорь5002  30.06.2019 23:00
Монета бросается 100 раз. какова вероятность того, что герб откроется ровно 45 раз?...

Популярные вопросы