По комбинаторике, считающаяся сложной для 7 класса одной из лучших в москве школ. нужно решить! за круглым столом были приготовлены 12 мест для жюри с указанием имени на каждом месте. дмитрий, пришедший первым, сел не на свое, а на следующее по часовой стрелке место. каждый член жюри, приходивший к столу после этого, занимал свое место или, если оно уже было занято, шел вокруг стола по часовой стрелке и садился на первое свободное место. возникшее расположение членов жюри зависит от того, в каком порядке они подходили к столу. сколько может возникнуть различных рассадки жюри?
Ответы
Пусть члены жюри как-то сели за стол. Занумеруем их по часовой стрелке, начиная от Николая Николаевича. Затем удалим всех, кроме Николая Николаевича, из-за стола и будем запускать их обратно в порядке их номеров. Рассадка при такой операции не изменится. Таким образом, можно считать, что члены жюри заходят в таком порядке, что занимают места за столом по часовой стрелке. Занумеруем места за столом по часовой стрелке так, чтобы место, где должен был сесть Николай Николаевич, имело номер 12 (т.е. Николай Николаевич сел на первое место). Пусть в некоторый момент за столом заняты k мест и k < 11. Тогда в этот момент никто из тех, кто должен занять места от k + 1 до 11, еще не пришел. А всего еще не пришло 12 – k членов жюри, значит еще не пришел только один человек, чье место уже занято. Следовательно, на место номер k + 1 может сесть один из двух еще не пришедших членов жюри: либо тот, чье это место, либо тот, чье место уже занято. Таким образом, каждое место с номером от 2 до 11 может быть занято двумя а место номер 12 одним Следовательно, всего может возникнуть 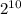 рассадки членов жюри.
рассадки членов жюри.
ПОКАЗАТЬ ОТВЕТЫ
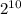 рассадки членов жюри.
рассадки членов жюри.
Другие вопросы по теме Математика
Популярные вопросы
- Приведите пример культуротранслирующей функции религии...
2 - Запиши предложения в соответствующие колонки. Реши орфографические...
3 - Вычеслите массу 9 моль цинк гидрооксида...
2 - Передатчик установленный на борту космического корабля работает...
3 - Площадь сечения, параллельного дну пирамиды, и площадь дна рассматриваются...
2 - У хлопчика є певна кількість грошей, за яку він може придбати...
1 - РУССКИЙ ЯЗЫК НАЙДИТЕ ПРЕДЛОЖЕНИЕ,СООТВЕТСВУЮЩИЕ ДАННЫМ В СПРАВКЕ...
1 - Teenagers and Drugs Two separate surveys suggest that Britain’s...
3 - Із даху будинку на висоті 45 м випущено горизонтально стрілу...
3 - Объясните, почему набор поясов на Урале разный. ...
3