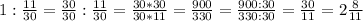Первая бригада может выполнить работу за 5 часов а вторая за 6 часов за сколько часов могут выполнить работу обе бригады работая вместе
Другие вопросы по теме Математика
Популярные вопросы
- Найдите значения выражения ,с объяснение , если можно16/3 +1)*6+(1/2)^2...
1 - 14. выполни деление с остатком. 65: 7= 15: 13= 91: 9= 56: 25=...
2 - I. замените в следующих предложениях действительный залог страдательным. переведите...
1 - Переведите: cool school uniform. think of a uniform for your school or for your...
3 - Объём лёгких у спортсменов в 2 раза больше ,чем у людей, не занимаюшихся спортом....
2 - На сковородку одновременно можно положить 2 карася, чтоб поджарить одного карася...
1 - 33.6 л сероводорода сожгли в избытке кислорода выход продукта составляет 75процентов,...
2 - Слово притворно найти близкое по значению...
2 - Сосна обыкновенная в природном сообществе выполняет роль 1. производителя органического...
3 - Синтаксический разбор . там, в глубине одного из небольших дворов, мы облюбовали...
2
1)1:5=1/5(раб.)-производительность первой бригады в час
2)1:6=1/6(раб.)-производительность второй бригады в час
3)1/6+1/5=11/30(раб.)-производительность двух бригад вместе за час
4)1:11/30=30/11=2 8/11(ч.)-сделают работу две бригады вместе
ответ: 2 8/11 часа.
Работая вместе, обе бригады могут закончить работу за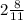 часа.
часа.
Пошаговое объяснение:
Узнаем производительность первой бригады:
1) ( р. ) - производительность первой бригады.
( р. ) - производительность первой бригады.
Узнаем производительность второй бригады:
2)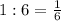 ( р. ) - производительность второй бригады.
( р. ) - производительность второй бригады.
Узнаем совместную производительность:
3)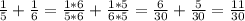
Узнаем время совместной работы:
4)