Параллелограмм - математика
Другие вопросы по теме Математика
Популярные вопросы
- Чаще всего бывает красно-коричневого цвета во влажном состоянии хорошо лепится...
1 - Напишите сочинение на тему як страшна стала яго имя (на языке) по магила льва...
1 - Напишите предложения что можно не делать в летние каникулы write what you...
2 - Назовите основные права граждан российской федерации....
2 - 5м-5дм, 5м-5см, 5м 6дм-8дм, 5м 6см-8см, 1кг-200г, 2м: 5. найди значений выражений?...
3 - Коли помер ы народився григір тютюнник?...
1 - Вместо пустой клетки поставить нужные цифры. ( пустые клетки буду обозначать...
1 - Подберите 5 предложений с разными цитирования....
1 - 5предложений из художественной со словами в которых есть суффиксы ова,ева,ива,ыва....
2 - Носов приключения незнайки и его друзей какой это рассказ сатиристический...
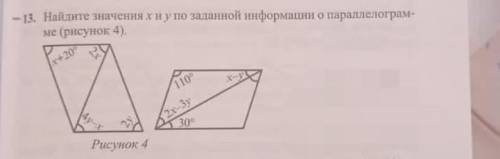
1
1)учитывая, что противоположные и накрест лежащие углы у него равны будет система
x+20=2y
2x=4y-x
дальше методом подстановки
x=2y-20 из первого и во второе
2(2y-20)=4y-(2y-20)
4y-40=4y-2y+20
2y=60
y=30
x=60-20=40
2)из равенства накрест лежащих углов
x-y=30
и второе уравнение системы про сумму углов в треугольнике
2x-3y+110+x-y=180; 3x-4y=70
Два подчеркнутых уравнения образуют систему, из первого х=30+у и во второе
3(30+y)-4y=70
90-y=70
y=20
x=30+20=50
Пошаговое объяснение:
Для удобства обозначим на обоих рисунках вершины параллелограмма АВСД.
№1
Противоположные углы параллелограмма равны, поэтому ∠В=∠Д, а ∠ВАС=∠АСД как внутренние разносторонние, составим систему уравнений, используя это свойство:
х+20=2у
2х+х=4у
х=2у–202х+х=4ух=2у–20
3х=4у
Подставим значение х во уравнение:
3х=4у
3(2у–20)=4у
6у–60–4у=0
2у=60
у=60÷2
у=30
Теперь подставим значение у в уравнение:
х=2у–20=2×30–20=60–20=40
х=40; у=30
Теперь подставим значения х и у в выражения углов:
В ∆АВС:
∠АВС=х+20=40+20=60°
∠АСВ=2х=2×40=80°
Сумма углов любого треугольника равна 180°
∠ВАС=180–60–80=40°
В ∆АСД:
∠САД=4у–х=4×30–40=120–40=80°
∠АДС=2у=2×30=60°
∠АСВ=∠АСД=40°
ОТВЕТ: ∠АВС=∠АДС=60°; ∠АСВ=САД=80°; ∠ВАС=∠АСД=40°; х=40, у=30
№2
Противоположные углы параллелограмма равны, то ∠В=∠Д=110°.
Рассмотрим ∆АСД, Сумма углов любого треугольника равна 180°, поэтому ∠САД+∠АСД+∠Д=180°, тогда:
∠АСД=180–∠САД–∠Д=180–30–110=180–140=40°
∠АСВ=∠САД и ∠ВАС=∠АСД как внутренние разносторонние.
Согласно этим равенствам составим систему уравнений:
х–у=30
2х–3у=40
х=30+у2х–3у=40Подставим значение х во второе уравнение:
2х–3у=40
2(30+у)–3у=40
60+2у–3у=40
–у=40–60
–у= –20 |×(–1)
у=20
Подставим значение у в уравнение:
х=30+у=30+20=50
х=50; у=20
Теперь подставим значения х и у в выражения углов:
∠ВАС=∠АСД=2х–3у=2×50–3×20=100–60=40°
∠АСВ=∠САД=х–у=50–20=30°
ОТВЕТ: х=50, у=20, ∠ВАС=∠АСД=40°, ∠АСВ=∠САД=30°