ответте на вопрос не скопируй от предыдущего ответа,

(если не правилно тому бан)!

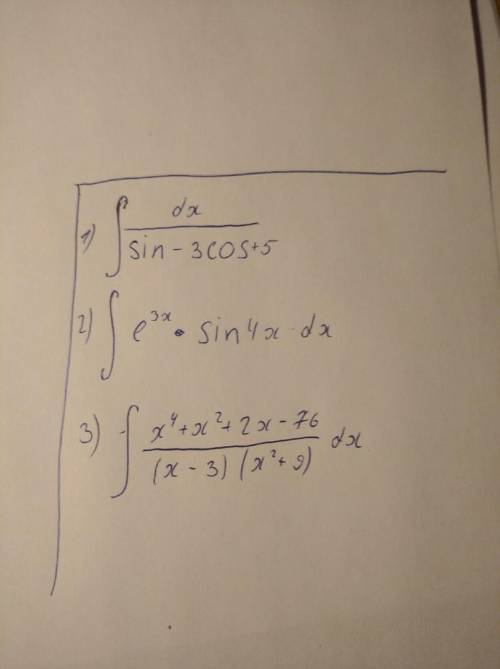
ответте на вопрос не скопируй от предыдущего ответа, (если не правилно тому бан)!

Ответы

mondy358 24.04.2021 11:10

Пошаговое объяснение:

$\int\limits \frac{dx}{ \sin(x) - 3 \cos(x) + 5} \\$

Тригонометрическая замена:

$t = tg \frac{x}{2} \\ \sin(x) = \frac{2t}{t {}^{2} + 1} \\ \cos(x) = \frac{1 - {t}^{2} }{1 + {t}^{2} } \\ dx = \frac{2dt}{t {}^{2} + 1}$

$\int\limits \frac{2dt}{t {}^{2} + 1 } \times \frac{1}{ \frac{2t}{t {}^{2} + 1} - \frac{3(1 - {t}^{2}) }{1 + {t}^{2} } + 5 } = \\ = \int\limits\frac{2dt}{t {}^{2} + 1} \times \frac{ {t}^{2} + 1 }{2t - 3(1 - {t}^{2}) + 5( {t}^{2} + 1) } = \\ = 2\int\limits \frac{dt}{2t - 3 + 3 {t}^{2} + 5 {t}^{2} + 5} = \\ = 2\int\limits \frac{dt}{2t + 8 {t}^{2} + 2 } = \int\limits \frac{dt}{4t {}^{2} + t + 1} \\ \\ \\ 4 {t}^{2} + t + 1 = \\ = {(2t)}^{2} + 2t \times 2 \times \frac{1}{4} + \frac{1}{16} + \frac{15}{16} = \\ = {(2t + \frac{1}{4}) }^{2} + {( \frac{ \sqrt{15} }{4}) }^{2} \\ \\ \\ \int\limits \frac{dt}{ {(2t + \frac{1}{4}) }^{2} + ( \frac{ \sqrt{15} }{4}) {}^{2} } = \frac{1}{2} \int\limits \frac{d(2t + \frac{1}{4}) }{ {(2t + \frac{1}{4} )}^{2} + ( \frac{ \sqrt{15} }{4}) {}^{2} } = \\ = \frac{1}{2} \times \frac{1}{ \frac{ \sqrt{15} }{4} } arctg \frac{(2t + \frac{1}{4} )}{ \frac{ \sqrt{15} }{4} } + c = \\ = \frac{2}{ \sqrt{15} }arctg( \frac{8t + 1}{ \sqrt{15} }) + c = \\ = \frac{2}{ \sqrt{15} } arctg( \frac{8tg \frac{x}{2} + 1}{ \sqrt{15} } ) + c$

$\int\limits {e}^{3x} \sin(4x) dx \\$

Интеграл с реккурентной формой.

Решим по частям:

$u = \sin(4x) \: \: \: \: \: \: \: du = 4 \cos(4x) dx \\ dv = {e}^{3x} dx \: \: \: v = \frac{1}{3} \int\limits {e}^{3x} dx = \frac{ {e}^{3x} }{3} \\ \\ uv - \int\limits \: vdu = \\ = \frac{ {e}^{3x} }{3} \sin(4x) - \frac{4}{3} \int\limits {e}^{3x} \cos(4x) dx \\ \\ \\ u = \cos(4x) \: \: \: \: du = - 4 \sin(4x) dx \\ dv = {e}^{3x} \: \: \: \: v = \frac{ {e}^{3x} }{3} \\ \\ \\ \frac{ {e}^{3x} }{3} \sin(4x) - \frac{4}{3}( \frac{ {e}^{3x} }{3} \cos(3x) + \frac{4}{3} \int\limits {e}^{3x} \sin(4x) dx) = \\ = \frac{ {e}^{3x} }{3} \sin(4x) - \frac{4 {e}^{3x} }{9} \cos(3x) - \frac{16}{9} \int\limits {e}^{3x} \sin(4x) dx$

Получили исходный интеграл

Возьмём его за I

Тогда:

$i = \frac{ {e}^{3x} }{3} \sin(4x) - \frac{4e {}^{3x} }{9} \cos(4x) - \frac{16}{9} i \\ i + \frac{16}{9} i = {e}^{3x} \times \frac{1}{3} ( \sin(4x) - \frac{4}{3} \cos(4x) ) \\ \frac{25}{9} i = \frac{ {e}^{3x} }{3} ( \sin(4x) - \frac{4}{3} \cos(4x) ) \\ i = \frac{9}{25} \times \frac{ {e}^{3x} }{3} ( \sin(4x) - \frac{4}{3} \cos(4x) ) \\ i = \frac{3 {e}^{3x} }{25} ( \sin(4x) - \frac{4}{3} \cos(4x) )$

$\int\limits {e}^{3x} \sin(4x) dx = \frac{3 {e}^{3x} }{25} ( \sin(4x) - \frac{4}{3} \cos(4x) ) + c\\$

$\int\limits \frac{ {x}^{4} + {x}^{2} + 2x - 76 }{(x - 3)( {x}^{2} + 9)}dx = \int\limits\frac{ {x}^{4} + {x}^{2} + 2x - 76 }{ {x}^{3} + 9x - 3 {x}^{2} - 27} dx \\$

Дробь неправильная, выделим целую часть:

$= \int\limits(x + 3 + \frac{ {x}^{2} + 2x + 5}{(x - 3)( {x}^{2} + 9) } )dx = \\ = \int\limits(x + 3)dx + \int\limits \frac{ {x}^{2} + 2x + 5}{(x - 3)( {x}^{2} + 9) } dx \\ \\ 1)\int\limits(x + 3)dx = \frac{ {x}^{2} }{2} + 3x + c \\ \\ 2) \frac{ {x}^{2} + 2x + 5 }{(x - 3)( {x}^{2} + 9) } dx$

С неопределенных коэффициентов:

$\frac{ {x}^{2} + 2x + 5}{(x - 3)( {x}^{2} + 9) } = \frac{a}{x - 3} + \frac{bx + c}{ {x}^{2} + 9} \\ {x}^{2} + 2x + 5 = a( {x}^{2} + 9) + (bx + c)(x - 3) \\ {x}^{2} + 2x + 5 =a {x}^{2} + 9a + b {x}^{2} - 3bx + cx - 3c \\ \\ 1 = a + b \\ 2 = - 3b + c \\ 5 = 9a - 3c \\ \\ a = \frac{10}{9} \\ b = - \frac{1}{9} \\ c = \frac{15}{9}$

Получаем:

$\frac{10}{9} \int\limits \frac{dx}{x - 3} - \frac{1}{9} \int\limits \frac{x - 15}{ {x}^{2} + 9 } dx = \\ = \frac{10}{9} ln( |x - 3| ) - \frac{1}{9} \int\limits \frac{xdx}{ {x}^{2} + 9} + \frac{15}{9} \int\limits \frac{dx}{ {x}^{2} + 9 } = \\ = \frac{10}{9} ln( |x - 3| ) - \frac{1}{9 \times 2} \int\limits \frac{2xdx}{ {x}^{2} + 9} + \frac{15}{9} \int\limits \frac{dx}{ {x}^{2} + {3}^{2} } = \\ = \frac{10}{9} ln( |x - 3| ) - \frac{1}{18} \int\limits \frac{d( {x}^{2} + 9)}{ {x}^{2} + 9 } + \frac{15}{9 \times 3} arctg( \frac{x}{3} ) + c = \\ = \frac{10}{9} ln( |x - 3| ) - \frac{1}{18} ln( | {x}^{2} + 9 | ) + \frac{5}{9}arctg( \frac{x}{3} ) + c$