Отметьте 9 точек на звезде при следующих условиях: 1.через точку ходить можно
2.с точки движения нет
3.на третий счёт ставится точка
4.хождение по прямой линии
Это задача на логику, она связана с математикой
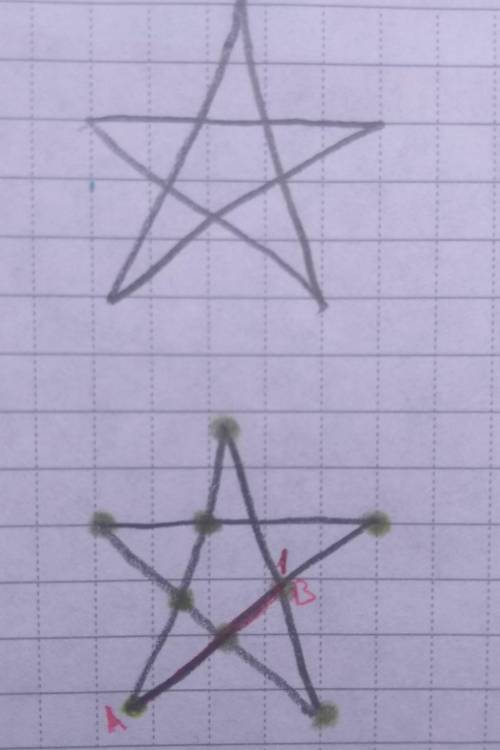
Ходить можно от любой точки, обозначенной зелёным цветом(там я одну случайно не обозначила).На 2 звезде изображён один ход согласно условиям от точки A до B(теперь от точки номер 1 ход нельзя совершить)Всего нужно 9 точек.Как я заметила в звезде 9 треугольников, но это мало чем Надеюсь на вашу
​

Чтобы решить данную задачу, давайте последовательно выполним каждое из условий.

Условие 1: через точку ходить можно.
Это означает, что каждая точка может быть посещена, будь то направо, налево, вверх или вниз. Отметим все точки внутри и на границе звезды.

Условие 2: с точки движения нет.
Это значит, что нельзя делать движение от одной точки к другой внутри звезды. Это также означает, что мы не можем ходить на противоположную стророну от начальной точки. В данной задаче начальной точкой можно считать любую точку.

Условие 3: на третий счёт ставится точка.
Чтобы выполнить это условие, мы должны поставить точку после третьего хода от начальной точки.

Условие 4: хождение по прямой линии.
В этой задаче мы должны двигаться по прямым линиям между точками, а не делать повороты. Мы не можем ходить по диагонали между точками.

Теперь, с учётом всех этих условий, приступим к их выполнению.

1) Начнём с любой точки и отметим её. Назовём её "1".

2) Из этой точки можно пойти в две стороны - вправо и влево. Давайте пометим две точки справа и слева от неё. Назовём их "2" и "3".

3) Согласно третьему условию, на третий счёт ставится точка. Таким образом, из точки "2" мы можем пойти в две стороны. Давайте отметим точки "4" и "5".

4) После этого мы не можем делать ходы из точек "1" и "5" (согласно второму условию). Отметим эту информацию, чтобы не забыть.

5) Теперь повторяем шаги 2-4 для точки "3". Из этой точки мы можем пойти в две стороны и отметить точки "6" и "7".

6) После этого мы не можем делать ходы из точек "2" и "7". Отметим и эту информацию.

7) Наконец, повторяем шаги 2-4 для точки "4". Будем отмечать её точками "8" и "9".

Теперь мы отметили все 9 точек, удовлетворяющие данным условиям. Кроме того, заметим, что каждая из точек образует треугольник с остальными точками.

Оптимальный путь для обхода всех этих точек можно увидеть на изображении ниже:

Таким образом, ответ на задачу будет следующим:
Отметьте точки на звезде: 1, 2, 3, 4, 5, 6, 7, 8, 9.