Основания равнобедренной трапеции равны 10 и 20, а её боковые сто-
роны равны 13. найдите площадь трапеции.​

Площадь равна произведению полусуммы оснований на высоту. Если из вершин тупых углов верхнего основания опустить высоты, то отрезки, на которые рассекается нижнее основание, равны 5;10;5, т.к. трапеция равнобедренная. Высота равна √(13²-5²)=12

Площадь равна ((10+20)/2)*12=180

ответ:  180.  

Вот формула площади трапеции:

, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).

Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен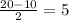 . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:  

Теперь высоту мы знаем и можем найти площадь трапеции:

Задача решена!