1. Математика
  2. Основанием прямой призмы является

Основанием прямой призмы является трапеция с основаниями 8 см и 33 см и боковыми сторонами 15 см и 20 см. Вычислить объём призмы, если её высота равна 15 см.

ŦøPňŷŦĩĩ78 ŦøPňŷŦĩĩ78    3   31.03.2020 00:12    5

Ответы
lesenok277 lesenok277  12.10.2020 10:03

Формула площади трапеции через стороны (вывод ниже):

    S=\frac{b+d}{2} \sqrt{a^2-\left( \frac{a^2 -c^2+(d-b)^2}{2(d-b)} \right) ^2}

    S= \frac{8+33}{2}\cdot\sqrt{15^{2}-\left(\frac{15^{2}-20^{2}+\left(33-8\right)^{2}}{2\left(33-8\right)}\right)^{2}} = \\= \frac{41}{2}\cdot\sqrt{225-\left(\frac{225-400+625}{50}\right)^{2}}=\\= \frac{41}{2}\cdot\sqrt{225-\left(\frac{450}{50}\right)^{2}} = \frac{41}{2}\cdot\sqrt{225-81}} = \frac{41}{2}\cdot 12 = 41\cdot 6 =246 \\\\S=246 \:\: (cm^2)

Объем прямой призмы равен произведению площади основания S на высоту призмы h:

    V= S\cdot h\\ V = 246\cdot 15 = 3690\\ \\ V = 3690 \:\: (cm^3)

ответ: Объем призмы равен 3690 см³.

_______________________________

Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с метода подстановки.

Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y. Таким образом x+y = d−b, y = d−b−x.

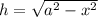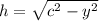Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту h=\sqrt{a^2-x^2} и h=\sqrt{c^2-y^2}. Приравнивая, получаем:

a²−x² = c²−y² или x²−y² = a²−c².

Подставляем вместо х полученное выше выражение d−b−x:

x²−(d−b−x)² = a²−c²

x²−d²+bd+dx-b²+bd−bx−x²+dx−bx = a²−c²

x²−d²+2bd+2dx−b²−2bx−x² = a²−c²

2dx−2bx = a²−c²+d²+b²−2bd

2x(d−b)=a²−c²+(d−b)²

x=\frac{a^2-c^2+(d-b)^2}{2(d-b)}

Подставляем обратно x в формулу высоты:

h=\sqrt{a^2-\left( \frac{a^2 -c^2+(d-b)^2}{2(d-b)} \right) ^2}

Формула площади трапеции через стороны будет выглядеть так:

S=\frac{b+d}{2} \sqrt{a^2-\left( \frac{a^2 -c^2+(d-b)^2}{2(d-b)} \right) ^2}


Основанием прямой призмы является трапеция с основаниями 8 см и 33 см и боковыми сторонами 15 см и 2
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Nikitakos222 Nikitakos222  19.07.2019 14:20
Мотоциклист и пешеход одновременно отправились навстречу друг другу.средняя скорость мотоциклиста 50км/ч,а пешехода 5 км/ч.на сколько километров они приблизятся за 1...
lenababkina200 lenababkina200  19.07.2019 14:20
Делитель 51 частное 40 чему равно делимое...
magiklen magiklen  19.07.2019 14:20
Вцветочный магазин 57 красных и белых роз. из красных роз сделали 3 больших букета по 9 роз в каждом. сколько белых роз в магазин?...
yanapetelyakp070y8 yanapetelyakp070y8  19.07.2019 14:20
Расстояние от минска до боровлян составляет третью часть расстояния от минска до логойска сколько километров от минска до боровлян если расстояние от минска до логойска...
Emmaff Emmaff  19.07.2019 14:20
Допишите так, чтобы равенство было верным: 1) 7,045=7 целых 45\? ; 2)4,? =4 целых 31\10000 3)0,0027=0 целых ? \10000 1) 7,045=7 целых 45/100 2) 4,0031=4 целых 31/10000...
Polika127 Polika127  19.07.2019 14:20
Протяженность реки иле протикающей по территории казахстана равна 814,75км за его приделами 624,25 км чему равна общая часть протяженность реки иле ? а) 1439км в) 1446км...
yyuyuy yyuyuy  19.07.2019 14:20
На координатном луче отмечены точки а (29,4) , в ( 93,5) и с.расстояние от точки с до точки а равно 25,6 единичного отрезка.найдите ав,ас и вс. сколько решений имеет...
мurr мurr  19.07.2019 14:20
19*х=1862, а: 35=245, 8: х=24: 6,86: 43=а: 1...
kamilaiks466 kamilaiks466  19.07.2019 14:20
Площадь прямоугольника 42 см.найди ширину прямоугольника если его длина 7 см .найди периметр прямоугольника...
luiza2010 luiza2010  19.07.2019 14:20
Число 82 умножили на половину от сотни сколько полочили...

Популярные вопросы