Основание наклонного параллелепипеда — квадрат со стороной 10 см. Боковое ребро AA1 = 7 см со сторонами AB и AD образовало равные острые углы. Определи длину диагонали DB1 (результат округли до одной десятой

ответ: 15,8

Пошаговое объяснение: Пространственная теорема Пифагора

Диагональ квадрата = a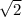 = 10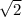

Теорема Пифагора: =+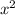

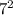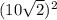
Добрый день! Давайте решим вместе эту задачу.

Для начала, давайте взглянем на рисунок и обозначим данные:

A и B - вершины основания параллелепипеда, АA1 - боковое ребро параллелепипеда, AD и DB1 - диагонали параллелепипеда.

Так как нам дано, что АA1 = 7 см, то это означает, что все стороны треугольника AAB1 равны 7 см.

Теперь мы можем применить теорему Пифагора для нахождения диагонали DB1.

Для этого нам необходимо выразить AD через AB и DB1. Обратите внимание, что треугольник ADB1 - прямоугольный, так как AD и DB1 являются диагоналями прямоугольника AAB1B.

Исходя из данных, длина AB равна стороне квадрата и составляет 10 см. Теперь нам нужно найти длину AD.

Так как в треугольнике AAB1 боковое ребро AA1 равно 7 см, то применим теорему косинусов:

AB^2 = AA1^2 + B1A^2 - 2 * AA1 * B1A * cos(угол A1AB)

Поскольку углы A1AB, A1BA и B1AA1 равны между собой (как острые углы в равнобедренном треугольнике), мы можем обозначить угол A1AB как x, и сказать, что B1AA1 = A1AB = A1BA = x.

Тогда уравнение будет выглядеть следующим образом:

AB^2 = AA1^2 + A1B^2 - 2 * AA1 * A1B * cos(x)

10^2 = 7^2 + A1B^2 - 2 * 7 * A1B * cos(x)

100 = 49 + A1B^2 - 14 * A1B * cos(x)

Теперь мы можем выразить A1B через AD и DB1, так как эти стороны составляют диагонали параллелепипеда:

A1B = AD^2 + DB1^2 - 2 * AD * DB1 * cos(x)

Теперь мы можем подставить это значение в предыдущее уравнение:

100 = 49 + (AD^2 + DB1^2 - 2 * AD * DB1 * cos(x))^2 - 14 * (AD^2 + DB1^2 - 2 * AD * DB1 * cos(x)) * cos(x)

100 = 49 + AD^2 + DB1^2 - 2 * AD * DB1 * cos(x) - 14 * (AD^2 + DB1^2 - 2 * AD * DB1 * cos(x)) * cos(x)

Мы не знаем значения угла x, поэтому пока оставим его в таком виде.

Теперь у нас получается квадратное уравнение, которое нам нужно решить относительно DB1.

100 = 49 + AD^2 + DB1^2 - 2 * AD * DB1 * cos(x) - 14 * (AD^2 + DB1^2 - 2 * AD * DB1 * cos(x)) * cos(x)

Выполним несколько преобразований:

0 = 39 + AD^2 + DB1^2 - 2 * AD * DB1 * cos(x) - 14 * AD^2 - 14 * DB1^2 + 28 * AD * DB1 * cos(x) * cos(x)

Теперь объединим подобные слагаемые:

0 = 39 - 13 * AD^2 - 13 * DB1^2 + 2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x))

0 = 39 - 13 * (AD^2 + DB1^2) + 2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x))

Заметим, что AD^2 + DB1^2 = ADB1^2, так как они являются двумя катетами прямоугольного треугольника ADB1. Заменим это выражение:

0 = 39 - 13 * ADB1^2 + 2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x))

Теперь у нас есть квадратное уравнение, которое мы можем решить относительно ADB1.

ADB1^2 - 2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x)) - 39 = 0

Решим это квадратное уравнение. Применим дискриминант, чтобы найти значения ADB1:

D = (-2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x)))^2 - 4 * 1 * (-39)

ADB1 = (-(-2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x))) ± √((-2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x)))^2 - 4 * 1 * (-39))) / (2 * 1)

ADB1 = (2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x)) ± √((2 * AD * DB1 * (cos(x) - 14 * cos(x) * cos(x)))^2 - 4 * (-39))) / 2

ADB1 = AD * DB1 * (cos(x) - 14 * cos(x) * cos(x)) ± √(AD^2 * DB1^2 * (cos(x) - 14 * cos(x) * cos(x))^2 + 4 * 39) / 2

Теперь, чтобы найти конкретное значение ADB1, мы должны знать значения AD, DB1, cos(x) и угла x. Однако, нам не дано значение cos(x) или x, поэтому мы не можем решить точно уравнение.

Однако, если у нас есть значения AD и DB1, мы можем использовать угол AAD1 (который является углом между AD и AA1) для приближенного решения.

То есть, ADB1 ≈ AD * DB1 * (cos(AAD1) - 14 * cos(AAD1) * cos(AAD1)) ± √(AD^2 * DB1^2 * (cos(AAD1) - 14 * cos(AAD1) * cos(AAD1))^2 + 4 * 39) / 2.

Теперь, если у нас есть конкретные значения AD и DB1, мы можем подставить их и получить более точное приближенное значение ADB1 и округлить до одной десятой.

Надеюсь, этот ответ был достаточно подробным и понятным для вас. Если у вас есть еще вопросы, не стесняйтесь задавать!