1. Математика
  2. Определить сходимость/расходимость

Определить сходимость/расходимость ряда (ln n)/n^7. с решением.

СофияГольдина СофияГольдина    3   01.10.2019 07:20    0

Ответы
Daeshka88 Daeshka88  09.10.2020 07:18

∑_{n=2}^{∞}\frac{㏑(n)}{n^{7}}.

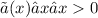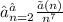Известно, что ㏑(x) ≤ x ∀x 0, так что \frac{㏑(n)}{n^{7}} ≤ \frac{n}{n^{7}} = \frac{1}{n^{6}}, так что если [tex]∑_{n=2}^{∞}\frac{1}{n^{6}} сходится, то и ∑_{n=2}^{∞}\frac{㏑(n)}{n^{7}} сходится.

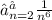Ряд ∑_{n=1}^{∞}\frac{1}{n^{p}} сходится, когда p > 1, значит ∑_{n=2}^{∞}\frac{1}{n^{6}} сходится, отсюда и исходный ряд сходится.

ответ: ряд сходится.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kitten0908 kitten0908  10.09.2019 23:30
Поезд едет со скоростью шесть седьмых км/мин .какое расстояние он проедет за пять шестых часа?...
втклр втклр  10.09.2019 23:30
Здрасти. с вопросом.найди закомерность 4, 6 , ,...
zveriok zveriok  10.09.2019 23:30
Найдите значение выражений используя арифметический закон а) 738-47-53 в) 62*11-62...
topciknazaraakinceva topciknazaraakinceva  10.09.2019 23:30
В5 а классе x учащихся, а в 5 б классе - на 2 учащихся больше. сколько всего учащихся в этих классах...
ladygum78 ladygum78  10.09.2019 23:30
Дайвер спортсмен прыгнув в воду с платформы высотой +2,2 м ,опустился до глубины -5 м. сколько метров составляет глубина погружения драйвера?...
LUKARIN LUKARIN  10.09.2019 23:30
Периметр квадратного поля равен км найди площадь в квадратных километрах...
диана2340 диана2340  10.09.2019 23:30
Найдите значение выражения 3,+y), если: 1)x=11,5 y=-2,2; 2) x=3,5; y= -2,25....
Ьрнрг Ьрнрг  10.09.2019 23:30
Дайвер спортсмен прыгнул в воду с платформы высотой +2,2 м , опустился на -5 м. сколько метро составляет глубина погружения драйвера?...
vbvb2006 vbvb2006  10.09.2019 23:30
Семь десятых частей 1 квадратных сантиметров...
Lolopoknhvkcgc Lolopoknhvkcgc  10.09.2019 23:30
Вычислите значения выражения удобным используя свойства сложения и вычитания: 1278+432+568 32*17+68*17 123*4*25 708-342-208 2132+231-132 786*115-86*115...

Популярные вопросы