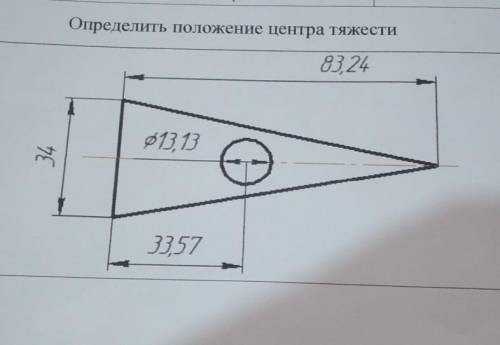
Определить положение центра тяжести ​

1) Площадь фигуры Δ (без выреза) ? Вы ,конечно, определите по известной формуле площади Δ как: (34×83,24):2=1415,08(это s1)

2) Теперь нужно определить площадь выреза. Естественно Вы определите её как: (π×D²):4=[π×(13,13)²]:4=  -135,4( это s2)

3) Тогда площадь материала Δ с учётом выреза: s1+s2=1415,08+(-135,4)=1279,68 (это S )

4) Вы, конечно, помните, что Ц.Т любого Δ лежит на пересечении его медиан. Заметим, что указанная на чертеже ось симметрии данной фигуры Δ совпадает с медианой, и по логике, на этой же оси симметрии и будет лежать Ц.Т  Δ. Остаётся найти общую точку пересечения двух других медиан с осью симметрии Δ (тоже медианой).

5) Известно, что точка пересечения медиан Δ делит эти медианы в отношении 2: 1 начиная от вершины(откуда проведена медиана). Значит(83,24:3)·1=27,746(от стороны равной 34)(обозначим как х1). Это Ц.Т Δ без выреза, центр отсчёта наших дальнейших вычислений(запомните это!!)

6) Тогда Ц.Т выреза (казалось бы абсурдное понятие, как может быть центр тяжести у пустоты выреза?!) по оси симметрии находится от Ц.Т Δ (без выреза) на расстоянии 33,57-27,746=5,824(это х2)

7) И теперь, по известной формуле, найдём Х- расстояние до Ц.Т Δ уже с учётом выреза:

   Х= [х1·s1+х2·s2]:S ⇒ [0·1415,08+5,824·(-135,4)]:1279,68= -0,616( видно, что раз величина получилась отрицательная, то центр тяжести с учётом выреза сдвинулся влево по оси симметрии Δ от точки х1 на 0,61)

или отсчитывая Ц.Т Δ с вырезом от стороны Δ равной 34: 27,746-0,616=27,13

Пошаговое объяснение: