Определить корни уравнения графически и уточнить один из них итерационными методами (методом деления отрезка пополам, методом Ньютона, методом простой итерации) с точностью 0,01:
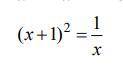
Другие вопросы по теме Математика
Популярные вопросы
- В приведенном перечне укажите понятие «выпадающее» из приведенного...
2 - Правильно ли подставлено полученное выражение в другое уравнение?...
1 - 6кл Подпишите картинки (Извините что есть надписи)...
3 - На чемпіонаті Республіки з важкої атлетики Іван Сила змагався з:...
2 - Перерізи кулі двома паралельними площинами, між якими лежить центр...
2 - Почему космонавты так боятся крошек...
2 - Чим здивована Череваниха щодо Гвинтовки? 2)Хто підтримує Сомка?...
3 - Знайдіть на осі z точку, рівновіддалену від точок А (-2; 0; 3) і...
3 - Из воды с глубины 5 м поднимают до поверхности камень объемом 60дм3....
1 - Төмендегі кестеде қазақ хандарының көршілес мемлекеттермен қарым-қатынасына...
3
На графике видно, что уравнение имеет два корня, один на отрезке [-3, -2] и второй на отрезке [1, 2]. Давайте начнем с первого корня:
1. Корень на отрезке [-3, -2]:
- Возьмем середину этого отрезка, т.е., значение x = (-3 + (-2)) / 2 = -2.5.
- Подставим значение x = -2.5 в уравнение и вычислим значение функции: f(-2.5) = (-2.5)^3 + 3(-2.5) - 3 = -7.375.
- Т.к. значение функции f(-2.5) отрицательное, то корень находится справа от -2.5.
- Возьмем новый отрезок [-2.5, -2].
- Повторим предыдущие шаги, подставив новое значение x и вычислив значение функции.
- Продолжим делить отрезок пополам и вычислять значение функции до тех пор, пока значение функции не станет достаточно близким к 0 или пока не достигнем нужной точности.
2. Корень на отрезке [1, 2]:
- Перейдем к этому корню и проделаем аналогичные шаги, как описано выше. Возьмем середину этого отрезка, вычислим значение функции и сравним с 0.
- Продолжим делить отрезок пополам и вычислять значение функции до тех пор, пока не достигнем нужной точности.
Теперь рассмотрим уточнение одного из найденных корней итерационными методами.
Метод деления отрезка пополам:
1. Возьмем один из корней, например, корень на отрезке [1, 2].
2. Найдем середину отрезка между 1 и 2, т.е. x = (1 + 2) / 2 = 1.5.
3. Подставим значение x = 1.5 в уравнение и вычислим значение функции: f(1.5) = (1.5)^3 + 3(1.5) - 3 = 4.875.
4. Используя значение функции f(1.5), определим новый отрезок, в котором находится корень:
- Если значение функции положительное, то корень находится слева от x=1.5. Возьмем новый отрезок [1, 1.5].
- Если значение функции отрицательное, то корень находится справа от x=1.5. Возьмем новый отрезок [1.5, 2].
5. Повторим шаги 2-4, пока не достигнем нужной точности или значение функции не будет достаточно близким к 0.
Метод Ньютона:
1. Выберем один из корней, например, корень на отрезке [1, 2].
2. Возьмем начальное приближение для корня, например, x0 = 1.5.
3. Вычислим значение функции и ее производную в точке x0: f(x0) и f'(x0).
4. Используем формулу Ньютона для приближенного вычисления нового значения x1: x1 = x0 - f(x0) / f'(x0).
5. Подставим значение x1 в уравнение и проверим, достигнута ли нужная точность. Если нет, то примем x1 как новое значение x0 и повторим шаги 3-5.
Метод простой итерации:
1. Выберем один из корней, например, корень на отрезке [1, 2].
2. Возьмем начальное приближение для корня, например, x0 = 1.5.
3. Выразим x1 из уравнения в виде x1 = g(x0), где g(x) - некоторая функция.
4. Подставим значение x0 в функцию g(x) и получим новое значение x1.
5. Проверим достигнута ли нужная точность, если нет, то примем x1 как новое значение x0 и повторим шаги 3-5.
Таким образом, путем графического определения корней уравнения и использования итерационных методов мы сможем уточнить один из корней с нужной точностью 0,01.