Определить коэффициенты А и В уравнения x^2+Ax+B=0, если известно, что А и В являются его корнями

Відповідь

Покрокове пояснення:

 - наше квадратне рівняння

 - загальне квадратне рівняння

Виходить, що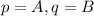

А з умови здачі маємо, що:

 - корені

Тоді, за теоремою Вієта маємо:

⇒ (1)

⇒ (2)

З рівняння (2) визначаємо A:

⇒ ⇒

З рівняння (1) визначаємо B:

⇒ ⇒  підставляємо в це рівняння значення A=1

Виходить ⇒

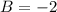
Можна зробити перевірку щоб впевнитись у правильності відповіді, підставляючи A та B в наше рівняння, отримаємо:

і за дискримінантом розв'язуємо це рівняння

Коефіцієнти правильні, тобто дорівнюють кореням