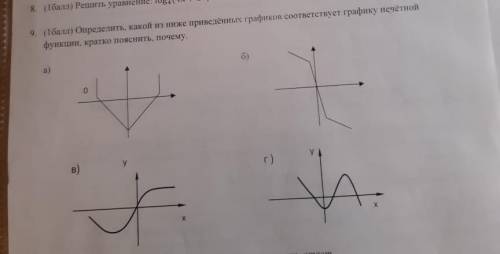
Определить, какой из нижеприведённых графиков, соответствует графику НЕЧЕТНОЙ функции

Добрый день! Давайте разберемся вместе.

Функция называется нечетной, если для любого числа x, f(-x) = -f(x). Это означает, что если мы возьмем любое значение x, и заменим его на противоположное (-x), то значение функции в этих точках должно быть противоположным.

Давайте рассмотрим каждый из графиков по очереди и определим, соответствуют ли они нечетной функции.

1. График A:

Посмотрим на точку (-1, 2). Если функция является нечетной, то ее значение для этой точки должно быть противоположным значению в точке (1, 2). Однако, на графике видно, что значения в этих точках одинаковые. Значит, график A не соответствует нечетной функции.

2. График B:

Рассмотрим точку (-1, -3). Если функция нечетная, то значение в этой точке должно быть противоположным значению в точке (1, 3). На графике видно, что это условие выполняется. Значит, график B может соответствовать нечетной функции.

3. График C:

Посмотрим на точку (-1, 1). Если функция нечетная, то значение в этой точке должно быть противоположным значению в точке (1, -1). Однако, на графике видно, что значения в этих точках одинаковые. Значит, график C не соответствует нечетной функции.

4. График D:

Рассмотрим точку (-1, -4). Если функция нечетная, то значение в этой точке должно быть противоположным значению в точке (1, 4). На графике видно, что это условие выполняется. Значит, график D может соответствовать нечетной функции.

Итак, график B и график D могут быть графиком нечетной функции.

Но как мы можем точно сказать, кто из них это? Для этого давайте посмотрим на точку (0, 0), так как у всех нечетных функций значение в этой точке должно быть равно 0. На графике B видно, что это условие выполняется, в то время как на графике D значение в точке (0, 0) не равно 0.

Таким образом, график B соответствует графику нечетной функции, а график D - не соответствует.

Надеюсь, я смог объяснить это понятно. Если у вас есть еще вопросы, не стесняйтесь задавать!