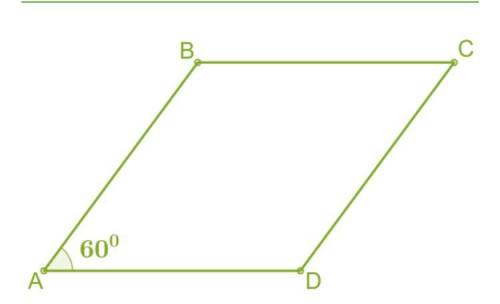
Определи скалярное произведение векторов, если сторона ромба ABCD равна 9 см

Скалярное произведение векторов а и ва*в=IaI*IвIcosα1) ВС*ДС=3*3*cos60°=9*cos60°=9*0,5=4,52) ВС*СД=3*3*сos120°=3*3*cos(180-60)=-9*cos60°=-4,5.

Для определения скалярного произведения векторов, нам необходимо знать координаты этих векторов.

В данном случае, у нас есть вектор AB и вектор AD. Для определения координат этих векторов, нам нужно знать длину сторон ромба.

У нас дано, что сторона ромба ABCD равна 9 см. Это означает, что все стороны ромба одинаковой длины.

Для начала, вектор AB - это вектор, направленный от точки A до точки B. Вектор AD - это вектор, направленный от точки A до точки D.

Так как сторона ромба ABCD равна 9 см, то можно предположить, что стороны AB и AD также равны 9 см.

Теперь, чтобы определить координаты этих векторов, нам нужно знать начальную точку, к которой они относятся.

Давайте предположим, что точка A имеет координаты (0, 0) на плоскости. Тогда, координаты точек B и D будут (9, 0) и (0, 9) соответственно, так как эти точки находятся на расстоянии 9 см от начальной точки A.

Теперь, чтобы определить координаты вектора AB, мы вычитаем координаты начальной точки A из координат конечной точки B:

AB = (координата конечной точки B) - (координата начальной точки A)
= (9, 0) - (0, 0)
= (9, 0)

Аналогично, чтобы определить координаты вектора AD, мы вычитаем координаты начальной точки A из координат конечной точки D:

AD = (координата конечной точки D) - (координата начальной точки A)
= (0, 9) - (0, 0)
= (0, 9)

Теперь, чтобы определить скалярное произведение векторов AB и AD, мы домножаем соответствующие координаты векторов и складываем их:

AB · AD = (координата x вектора AB) * (координата x вектора AD) + (координата y вектора AB) * (координата y вектора AD)
= 9 * 0 + 0 * 9
= 0

Таким образом, скалярное произведение векторов AB и AD равно 0. Это означает, что эти векторы ортогональны друг другу (перпендикулярны).