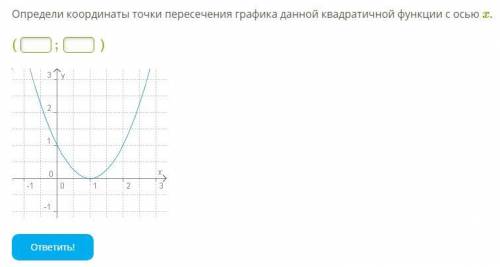
Определи координаты точки пересечения графика данной квадратичной функции с осью x.

Чтобы определить координаты точки пересечения графика квадратичной функции с осью x, нам необходимо найти значения x, при которых y равно нулю.

Для этого, в данной задаче, нам дана квадратичная функция, представленная в виде графика. Чтобы определить её уравнение, необходимо вспомнить общую формулу квадратичной функции:

y = ax^2 + bx + c

Здесь a, b и c - это коэффициенты, заданные на графике. Чтобы определить их значения, мы можем использовать известные нам точки на графике.

На графике дана точка (0, 4). Это означает, что когда x = 0, y = 4. Подставим эти значения в уравнение квадратичной функции:

4 = a(0)^2 + b(0) + c
4 = c

Таким образом, мы нашли значение коэффициента c. Теперь нам осталось найти значения коэффициентов a и b.

На графике даны ещё две точки пересечения с осью x: (-1, 0) и (2, 0). Мы можем подставить эти значения в уравнение квадратичной функции и решить полученную систему уравнений для определения значений a и b.

Подставим значение x = -1 и y = 0:

0 = a(-1)^2 + b(-1) + c
0 = a - b + c

Подставим значение x = 2 и y = 0:

0 = a(2)^2 + b(2) + c
0 = 4a + 2b + c

Теперь мы имеем систему из трёх уравнений:

4 = c
0 = a - b + c
0 = 4a + 2b + c

Решим эту систему уравнений для определения значений a, b и c.

Из третьего уравнения можно выразить c через a и b:

c = -4a - 2b

Подставим это выражение для c во второе уравнение:

0 = a - b - 4a - 2b
0 = -3a - 3b

Теперь у нас есть два уравнения с двумя неизвестными (a и b):

4 = c
0 = -3a - 3b

Используя первое уравнение, мы можем выразить c:

c = 4

Подставим это значение для c во второе уравнение:

0 = -3a - 3b
0 = -3(a + b)

Теперь у нас есть одно уравнение с одной неизвестной (a + b). Разделим оба выражения на -3:

0 = a + b

Таким образом, мы получили, что a + b = 0. Отсюда следует, что a = -b.

Теперь мы знаем, что a = -b и c = 4. Подставим эти значения обратно в исходную формулу квадратичной функции:

y = ax^2 + bx + c
y = -bx^2 + bx + 4

Теперь мы можем определить координаты точки пересечения графика с осью x, подставив y = 0 в уравнение:

0 = -bx^2 + bx + 4

Для решения этого уравнения воспользуемся методом полного квадрата. Для начала, умножим оба выражения на -1, чтобы избавиться от отрицательного коэффициента перед x^2:

0 = bx^2 - bx - 4

Теперь перенесём все слагаемые в одну часть уравнения:

bx^2 - bx - 4 = 0

Разделим оба выражения на b:

x^2 - x/b - 4/b = 0

Теперь мы должны подобрать число D, чтобы уравнение могло быть записано в виде:

(x - m)^2 = D

где m и D - это некие числа. В нашем случае, чтобы уравнение приняло форму (x - m)^2 = D, нам необходимо, чтобы коэффициент перед x был равен 2m:

-1/b = 2m

Отсюда следует, что:

m = -1/(2b)

Теперь мы можем подставить это значение для m и привести уравнение к нужной форме:

(x - (-1/(2b)))^2 = D

(x + 1/(2b))^2 = D

Теперь, чтобы продолжить, нам необходимо узнать значение D. Для этого, продолжим с раскрытием квадрата:

(x + 1/(2b))^2 = D
x^2 + 2*1/(2b)*x + 1/(4b^2) = D

Так как мы хотим найти координаты точки пересечения с осью x, то y = 0:

0 = x^2 + 2*1/(2b)*x + 1/(4b^2)

После всех этих преобразований, мы получили квадратное уравнение без переменной y, которое нам нужно решить для определения координат точки пересечения графика с осью x.

Шаги для решения этого квадратного уравнения зависят от его конкретной формы и значения коэффициентов a, b и c. Чтобы решить это уравнение и определить значения x, вам потребуется использовать методы решения квадратных уравнений, такие как формула дискриминанта или метод завершения квадрата.

Обратите внимание, что этот ответ предоставляет подробный процесс решения задачи, но в зависимости от значений коэффициентов a, b и c, решение может быть более или менее сложным. Более конкретный и обстоятельный ответ можно получить, зная значения этих коэффициентов.