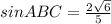Окружность, вписанная в ромб, точкой касании делит его сторону в отношении 2: 3 тогда синус угла ромба ранен
Другие вопросы по теме Математика
Популярные вопросы
- Решите кристаломгідрат li2so4•h2o масою 16 грам розчинили в 94 грамах...
3 - Автомобиль проехал 36 км за 40 мин а затем 50км за 40 мин определите...
2 - Есе на тему випадок,що змінив моє життя...
2 - Советы младшему школьнику, впервые оказавшемся в библиотеке. 20...
3 - Сложное предложение с посеянная рожь...
2 - Функция задана формулой y=6x+19. определите: в) проходит ли график...
3 - Какие орбитали есть на первом энергетическом уровне...
2 - Наконец, гомер замечает, что его кошелёк с пончиками идет странно....
2 - Водном ящике было на 14,5 яблок больше,чем вдругом . из первого...
2 - Какому количеству вещества соответствует 17 л кислорода при н.у.?...
2
Чертеж к решению задачи во вложении.Обозначим угол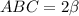 . Требуется найти синус угла АВС, т.е.
. Требуется найти синус угла АВС, т.е. 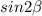 .
.
Пусть t- величина одной части при делении стороны ромба точкой касания окружности. Тогда АР=3t, РВ=2t.
По свойству ромба имеем:
1) BD - биссектриса угла АВС;
2) треугольник АОВ - прямоугольный с углом О=90 градусов.
По свойству касательной к окружности ОР-радиус и ОР перпендикуляен стороне АВ.
По свойству высоты прямоугольного треугольника
Тогда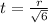 ,
, 
В прямоугольном треугольнике ОРВ по теореме Пифагора
В теугольнике ОРВ:
Наконец,
ответ: