Математика: Очень нужно, с подробным решением.

Очень нужно, с подробным решением.

Ответы

petrius100p0bmz5 11.10.2020 23:26

Модуль "Алгебра"

Задание 1

$21\cdot (\frac{1}{7})^2 - 10 \cdot \frac{1}{7} = (21\cdot\frac{1}{7} - 10)\cdot \frac{1}{7} = (\frac{21}{7} - 10) \cdot \frac{1}{7} = (3 - 10) \cdot \frac{1}{7} = -7\cdot \frac{1}{7} = -1$

Задание 2

$2x^2 + 5x - 12 = 0\\\\D = 25 + 12\cdot2\cdot4 = 12 + 96 = 108\\\\\sqrt{D} = 6\sqrt{3} \\\\ x_1 = \frac{-5+6\sqrt{3}}{4} = 6\sqrt{3} - 1,25\\\\x_2 = \frac{-5-6\sqrt{3}}{4} = -6\sqrt{3} - 1,25$

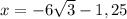
ответ: $x = -6\sqrt{3} -1,25$

Задание 3

$\frac{6}{x+6} = \frac{1}{x-4}\\\\x \neq -6\\\\ x \neq 4\\\\6(x - 4) = x+6\\\\6x - 24 = x+6\\\\6x - x = 6 + 24\\\\5x = 30\\\\x = 6$

Правильный ответ №1.

Задание 4

$(3- \sqrt2)^2 + 6\sqrt2 = 9 - 6\sqrt2 + 2 + 6\sqrt2 = 9 + 2 = 11$

Задание 5

Обозначим скорость течения за

$\frac{25}{17-x} = \frac{36}{17+x}\\\\25(17 +x) = 36(17-x)\\\\425+25x = 612 - 36x\\\\ 25x + 36x = 612 - 425\\\\61x = 187\\\\x = \frac{187}{61} \approx 3,06$

Модуль "Геометрия"

Задание 6

Первое утверждение неверно. Трапеция может быть обычной, равнобедренной или прямоугольной. Трапеция - четырёхугольник. И если все углы в четырёхугольнике равны, то это квадрат, а не трапеция.

Второе утверждение неверное, так как один из смежных углов является тупым, а второй острым.

Третье утверждение может быть верным, если речь идёт о прямоугольной трапеции.

Четвёртое утверждение неверно, так как один из смежных углов является тупым, а второй острым.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика