Очень нужно решить в виде pdf

(см. объяснение)

Пошаговое объяснение:

, ОДЗ: .

Выполним замену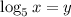 . Тогда .

Заметим сразу, что , так как .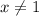

Тогда уравнение примет вид:

Так как , то верно, что .

С учетом этого перепишем уравнение:

Тогда перейдем к совокупности:

Рассмотрим первую строку совокупности:

Слева показательная функция. Она монотонно возрастает.

Справа гипербола. Она убывает на всей области определения.

Тогда рассматриваемое уравнение может иметь не более одного корня.

Несложно увидеть, что это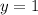 , так как при нем равенство верно.

Рассмотрим вторую строку совокупности:

Выполним теперь обратную замену:

Так, учитывая ОДЗ, мы получили, что и 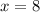- это корни исходного уравнения.

Задание выполнено!