очень нужно решение ,по методу Крамера и Гауса буду очень благодарна
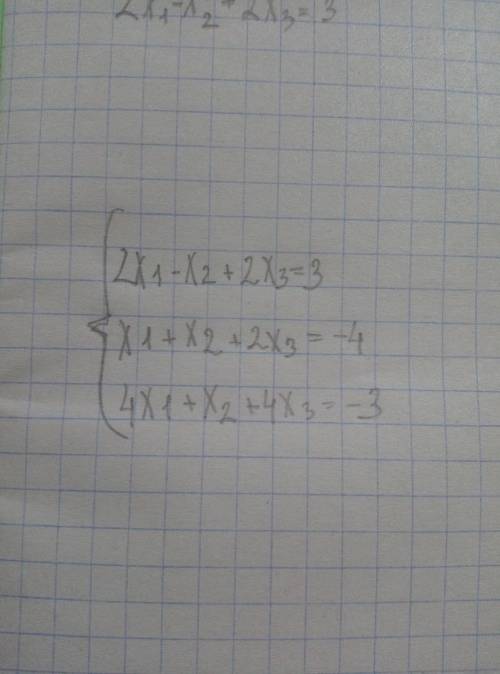
Другие вопросы по теме Математика
Популярные вопросы
- Розкрийте зміст поезії «Про коника та цвіркуна»...
1 - Схарактеризуйте вірші цього автора...
2 - Порівняйте сюжет про злу мачуху й добру пасербицю в «Казці про мертву...
2 - Які факти з життя Кітса вам запам яталися?...
3 - Визначте основну думку казки Уайльда «Хлопчик-зірка»...
3 - Перечитайте опис лісу, яким розпочинається казка Уайльда «Хлопчик-зірка»....
1 - Поясніть антитезу двох солов їв у казці Андерсена...
3 - Чим непохитний олов яний солдатик розсердив злого гнома?...
3 - Як було покарано Хлопчика-зірку з однойменної казки Уайльда?...
3 - Простежте за змінами в описах моря впродовж розвитку дії. Як ви пояснюєте...
2
ответ: x1=1, x2=-3, x3=-1.
Пошаговое объяснение:
1) Решение методом Гаусса.
1. Вычтем из первого уравнения второе и заменим первое уравнение этой разностью. Получим систему:
x1-2*x2=7
x1+x2+2*x3=-4
4*x1+x2+4*x3=-3
2. Умножим второе уравнение на 2, вычтем из него третье уравнение и заменим второе уравнение этой разностью. Получим систему:
x1-2*x2=7
-2*x1+x2=-5
4*x1+x2+4*x3=-3
3. Умножим второе уравнение на 2, прибавим к нему первое уравнение и заменим первое уравнение этой суммой. Получим систему:
-3*x1=-3
-2*x1+x2=-5
4*x1+x2+4*x3=-3
На этом прямой ход метода Гаусса завершён и начинается обратный ход:
1. Из первого уравнения находим x1=1.
2. Подставляя x1=1 во второе уравнение, находим x2=-3.
3. Подставляя x1=1 и x2=-3 в третье уравнение, находим x3=-1.
Проверка:
2*+3-2=3
1-3-2=-4
4-3-4=-3
Равенства превращаются в верные тождества - значит, решение найдено верно.
2) Решение методом Крамера.
1. Находим определитель системы:
Δ = 2 -1 2 =-6≠0 - значит, система имеет единственное решение.
1 1 2
4 1 4
2. Находим Δ1:
Δ1 = 3 -1 2 =-6
-4 1 2
-3 1 4
3. Находим Δ2:
Δ2= 2 3 2 = 18
1 -4 2
4 -3 4
4. Находим Δ3:
Δ3= 2 -1 3 = 6
1 1 -4
4 1 -3
5. Находим x1=Δ1/Δ=1, x2=Δ2/Δ=-3, x3=Δ3/Δ=-1.