ОЧЕНЬ НУЖНО 1. Найдите значение выражения sin a - 3cos a, если tg a = -2, 90° < a <180° 2. Определите, четна ли функция 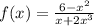
Другие вопросы по теме Математика
Популярные вопросы
- Тихий океан. площади: сравнение с другими океанами...
2 - Найдите неизвестные стороны и острые стороны треугольника по...
3 - Средний вес мальчиков того же возраста, что и коля, равен 60кг....
1 - Дві теплі течії,які додатково насичують повітря найвологішого...
2 - Дима съел 20% от торта, оля съела 15% от торта, владимир 46%,...
2 - Как узнать какой частью речи является слово?...
3 - Мини-сочинение из 5-7 односоставных предложений (можно 1-2 двусоставных)...
2 - (16/9)^х=(3/4)^5 в ответе получается -2,5...
3 - Решите тест по информатике 7 класс , 40 1)информация в компьютере...
3 - Тихий океан. площадь: сравнение с другими океанами...
1
Для решения этой задачи, мы сначала найдем значение sin a и cos a, а затем подставим их в данное выражение.
У нас дана информация, что tg a = -2. Мы знаем, что tg a = sin a / cos a, поэтому мы можем записать следующее:
sin a / cos a = -2
Затем мы можем возвести обе части уравнения в квадрат, чтобы избавиться от деления:
(sin a)^2 / (cos a)^2 = (-2)^2
sin^2 a / cos^2 a = 4
Теперь мы можем использовать основное тригонометрическое тождество, которое гласит:
sin^2 a + cos^2 a = 1
Из этого тождества мы можем получить следующее равенство:
4 + cos^2 a = 1
Теперь мы можем решить это уравнение:
cos^2 a = 1 - 4
cos^2 a = -3
Так как a находится в диапазоне от 90° до 180°, то cos a будет отрицательным числом. Из этого следует, что cos a = -√3.
Теперь мы можем найти значение sin a, используя уравнение sin^2 a + cos^2 a = 1:
sin^2 a + (-√3)^2 = 1
sin^2 a + 3 = 1
sin^2 a = 1 - 3
sin^2 a = -2
Так как sin a находится в диапазоне от 90° до 180°, то sin a будет положительным числом. Поэтому sin a = √2.
Теперь мы можем подставить значения sin a и cos a в данное выражение:
sin a - 3cos a = √2 - 3*(-√3) = √2 + 3√3
Ответ: значение выражения sin a - 3cos a равно √2 + 3√3.
2. Определите, четна ли функция f(x) = (6 - x^2) / (x + 2x^3):
Чтобы определить, является ли функция четной или нечетной, мы должны проверить, выполняется ли условие f(x) = f(-x) для всех значений x в области определения функции.
Для начала, найдем f(x):
f(x) = (6 - x^2) / (x + 2x^3)
Теперь заменим x на -x:
f(-x) = (6 - (-x)^2) / (-x + 2(-x)^3)
f(-x) = (6 - x^2) / (-x - 2x^3)
Мы видим, что f(x) и f(-x) не равны, поэтому функция f(x) не является ни четной, ни нечетной.
Ответ: функция f(x) = (6 - x^2) / (x + 2x^3) не является ни четной, ни нечетной.