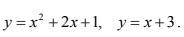
Другие вопросы по теме Математика
figa333
15.02.2022 09:23
eka445590226
15.02.2022 09:24
Dementor112
15.02.2022 09:37
dariapark1
15.02.2022 09:40
ХУХ00001
11.05.2020 15:42
Dbrfsdfsd
11.05.2020 15:41
jannamkrtchyan
11.05.2020 15:41
polyaХеХеХе
11.05.2020 15:41
Araikavipv
11.05.2020 15:42
Популярные вопросы
- Написать сочинение (150 слов), на тему: если бы я был художником,какую...
3 - 1. вычислите: а)4 целых 3/5 - 5 /7 ; б) 7/15 * 18/49 ; в) 0,2+ 2/3 ; г)...
1 - 81 84 80 83 83 79 найти закономерность и добавить 6 чисел...
3 - Укажите крупнейшие центры производства алюминия в россии...
3 - Втреугольнике mpc стороны mp имеют одну и ту же длину,равную 4 см,а сторона...
2 - Почему христианство так быстро завоевало сторонников в римской империи?...
3 - Anger is normal. or is it? in terms of frequency of expression anger is...
1 - Как сделать 4. вот уже золотие польсы протянулись по небу....
2 - Укажите верные утверждения: а) элемент атом которого на внешнем слое содержит...
1 - Переведите в указанные еденицы имерения 1 г см³= кг м³ 0.8 г см³= кг м³...
2
Найдем пределы интегрирования. для чего решим уравнение
х²+2х+1=х+3; х²+х-2=0; по Виету х=-2; х=1, значит, надо найти определенный интеграл от -2 до 1, от разности (х+3-(х²+2х+1))=-х²-х+2.
Это -х³/3-х²/2+2х
Подставляем пределы интегрирования и по формуле Ньютона - Лейбница находим площадь.
-1³/3-1²/2+2*1-(-(-2)³/3-(-2)²/2+2*(-2))=-1/3-1/2+2-8/3+2+4=4.5