Обязательно дайте объяснение.

На высоте неравнобедренного треугольника ABC, проведенной из вершины A, выбрана точка X.
Оказалось, что ∠ABX = ∠ACX. Докажите, что X совпадает с ортоцентром треугольника ABC.

Question

Математика: Обязательно дайте объяснение. На высоте неравнобедренного треугольника ABC, проведенной из вершины A, выбрана точка X. Оказалось, что ∠ABX = ∠ACX. Докажите, что X совпадает с ортоцентром треугольника ABC. ​

наука28 · Answer

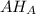Пусть AH_A — высота. Выполним симметрию ΔABX относительно AX. ΔABX переходит в ΔAB'X. ∠AB'X = ∠ACX и опираются на один отрезок, значит, AXB'C — вписанный четырёхугольник. Тогда и ∠B'CX = ∠B'AX. Но ΔBAB' — равнобедренный по построению, где 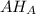AH_A — высота. Тогда ∠BAX = ∠B'AX = ∠B'CX.

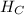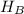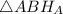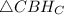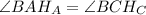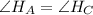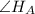Пусть прямая CX пересекает AB в H_C , а BX пересекает AC — в H_B . Рассмотрим $\triangle ABH_A$ и $\triangle CBH_C$ : ∠B — общий, $\angle BAH_A = \angle BCH_C$ ⇒ $\angle H_A = \angle H_C$ , но $\angle H_A$ — прямой, тогда и 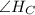$\angle H_C$ — прямой. 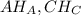AH_A, CH_C — высоты, пересекаются в точке X, тогда 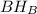BH_B — также высота, X — ортоцентр, что и требовалось доказать.

Обязательно дайте объяснение. На высоте неравнобедренного треугольника ABC, проведенной из вершины A

Популярные вопросы