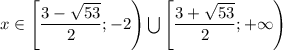Объясните как решать подобные неравенства(с корнями)? sqrt(x^2-3x-10)/(x+2)<=x-5
Я разложил подкоренное на множители:
sqrt((x+2)(x-5))/(x+2)<=x-5
привел к общему:
(sqrt((x+2)(x-5))-x^2+3x+10)/(x+2) <= 0
снова разложил на множители и *-1:
((x-5)(x+2)-sqrt((x+2)(x-5)))/(x+2) >=0
вынес за скобку:
(sqrt((x-5)(x+2))(sqrt((x-5)(x+2)) - 1))/(x+2) >=0
Но не знаю, что дальше делать. Вроде сократить нельзя, т.к х>-2
Другие вопросы по теме Математика
Популярные вопросы
- Лабораторная работа Влияние различных условий (температура, pH) на...
1 - Құбылыстарды танып білу үшін карталарды пайдалана отырып зерттеу...
3 - Задание 2 Читайте текст со словарем.Напишите основные данные.Во второй...
2 - ответить на вопросы Перевод: 1. Для чего нужна космос карта для космонавта?...
1 - Рассчитайте ускорение шарика по формуле 1 для каждого опыта результат...
1 - Казак халкынын ауа райы попс формула...
2 - Составьте словосочетания делать (что?) ......
1 - Напишите статью в газету по теме: Достопримечательности и путешествия...
3 - Если периметр параллелограмма равен 28 см, а стороны - 5 см, то на...
2 - Көліктің бұрылысы бар жолдарға қарағанда, түзу жолмен қозғалғандағы...
2
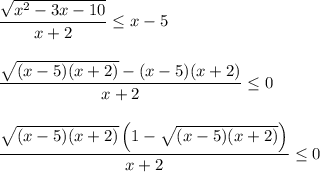
Из первого сомножителя числителя получим (объединим корни и ОДЗ):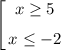
Корни второго сомножителя: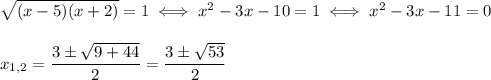
Из знаменателя:Теперь применим метод интервалов:
Поймем, где расположены корни второго сомножителя числителя: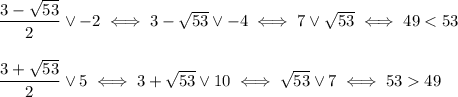
Применим метод интервалов, учтя, что, проходя через кореньответ.